2019年9月 | hk_cnyali's Blog

一点小记录

好题选讲做题记录

9-3

Process

代码能力还是太差，写T4写了一上午。T2、T3根本来不及看

以后还是要合理分配时间。。。

T1

随便搞，我是直接枚举 $[\lfloor \frac{n}{2}\rfloor - 3, \lfloor\frac{n}{2}\rfloor + 3]$ 内的数划分...

显然两个数差得越小越好

T2

[计数][容斥] [巧妙]

考虑和连通图计数类似的做法

设 $f_{i, j}$ 表示 $i$ 个点的连通图，每种方案为边数的 $j\in[0, 1, 2]$ 次幂的答案， $g_{i, j}$ 表示 $i$ 个点任意图的答案

显然， $j=0$ 时就是裸的连通图计数

f_{n, 0} = g_{n, 0} - \sum_{i=1}^{n - 1}\binom{n - 1}{i - 1}f_{i, 0} \times g_{n - i, 0}

考虑 $j=1$ ：

与 $j=0$ 类似的方法，前面都是一样的，只是最后一坨东西算法不一样

假设枚举出来的 $i$ 个点图的连边方案的边数为集合 $S$ ， $n-i$ 个点图的连边方案的边数为集合 $T$

那么我们就是要分别枚举 $S,T$ 中的元素，然后合并起来，即

\sum_{x\in S}\sum_{y\in T}(x + y)

化下式子：

\sum_{x\in S}x\times \Big(\sum_{y\in T}\Big) + \Big(\sum_{x\in S}\Big) \times \sum_{y\in T}y

到这一步就很显然了

f_{n, 1} = g_{n, 1} - \sum_{i=1}^{n - 1}\binom{n - 1}{i - 1}\Big(f_{i, 1} \times g_{n - i, 0} + f_{i, 0}\times g_{n - i, 1}\Big)

继续考虑 $j=2$ ：

\begin{aligned} &\sum_{x\in S}\sum_{y\in T}(x + y)^2\\ =&\Big(\sum_{x\in S}x^2\Big) \times \Big(\sum_{y\in T}\Big) + 2\Big(\sum_{x\in S}x\Big)\times\Big(\sum_{y\in T}y\Big) + \Big(\sum_{x\in S}\Big) \times \Big(\sum_{y\in T}y^2\Big) \end{aligned}

dp式子就不放了

然后考虑求 $g$ ，设 $m = \frac{i (i - 1)}{2}$

\begin{aligned} g_{i, 0} &= 2^m\\ g_{i, 1} &= m2^{m-1}\\ g_{i, 2} &= m2^{m-1} + m(m-1)2^{m-2}\\ \end{aligned}

解释一下

$j=1$ 时，考虑每条边的贡献，保证它出现，然后其他边随便选或不选的方案

$j=2$ 时，对于某个边数为 $d$ 的图，考虑把贡献看成的形式

即枚举图中的两条边，它们两的贡献是 $1\times1 = 1$ ，这样就把乘积转化为求和的形式了

讨论一下这两条边是否是同一条边

T3

[基环树] [动态规划] [背包]

首先，对于一条边 $(l_i, r_i, s_i)$ 而言，若被 $l_i$ 选，则权值为 $s_i$ ；否则为 $-s_i$

那么和这道题一样的转化后，显然是一棵基环树森林，每个基环树上只有可能是两种取值，假设它们为 $a, b(a > b)$

我们需要求出两种方案，一种的权值和在数轴上正方向最接近 $0$ ，另一种在负方向上最接近 $0$

先每个基环树都取 $a$ 权值（较大的），求出来的权值和在 $t$ 的位置

若 $t \le 0$ ，则再换小的肯定不会更优
若 $t > 0$ ，则有可能通过把某些 $a$ 换成 $b$ 之后， $t$ 会减小，且仍 $>0$

再抽象一下，即现在有若干个的物品（权值为 $a-b$ ），需要用它们填一个容积为 $t$ 的背包，问最多能填多少

因为权值比较小，重复的物品较多，所以跑多重背包即可

再对每个基环树取 $b$ 权值，做一遍类似操作即可，即从负方向逼近 $0$ 一次

T4

[k-d tree]

我直接写的三维k-d tree，过了

9-4

Process

三道题都比较简单，没有挂分。要继续保持

T1

我直接用的set+链表模拟，实际上就是求最长上升子序列的长度

T2

[动态规划] [字符串] [AC自动机]

$dp[i][j]$ 表示到填第 $i$ 位，从 $i - 4$ 至 $i$ 构成的数等于 $j$ 的方案数

转移的时候注意一下前导0

实际上也可以AC自动机做

T3

直接模拟，用BIT链加即可

9-5

Process

半个小时写完T1，想了很久的T2，无果，复习了一下SAM之后把T3写了。最后把T2写了个退火，获得了20分的好成绩

dp掌握的不太熟练，要多加练习

T1

[数学]

令 $a = E(A), b = E(B)$ ，则 $f[i] = f[i - 1] * a + b$

$ans = f[k]$

等比数列求和即可，比较简单

注意特判公比为 $1$ 的情况！！！

T2

[动态规划] [DP优化]

首先需要注意到，最终的01串中的每一个数字展开（还原后）是一系列不相交的区间！！！

于是可以区间dp，设 $f[i][j][S]$ 表示区间 $[i, j]$ ，合成的状态为 $S$ 的最大分数

因为区间长度确定，且每次操作后，长度都会减少 $K-1$ ，因此 $S$ 的位数是确定的

设 $len(i)$ 表示区间长度为 $i$ 时，最终合成的状态的长度，那么区间dp转移时枚举的 $k$ 需要满足 $len (k - i + 1) + len(j - k) \le K$

因此，所有 $>K$ 的状态都可以通过若干个 $\le K$ 的状态合并出来

再优化一下，发现只需要保证 $len(j - k) = 1$ 即可，道理是一样的

时间复杂度 $O(n^3 2^k)$ ，常数很小

一道dp好题！

只不过一开始的区间dp我就没想到，一开始觉得转移之间会有问题，就没去想了，自己yy了一个假做法

后面的一些优化都比较~~套路，只是我不会~~巧妙

T3

[字符串] [后缀自动机] [广义后缀自动机]

建广义SAM ，处理出 $size[i]$ 表示 $i$ 节点，只有 $S$ 串的传统节点有 $1$ 的贡献的子树大小 $\times$ $i$ 节点的 $maxlen - minlen$ ； $sum[i]$ 是 $i$ 到根的 $size$ 之和

在SAM上匹配 $T$ 串，找到每个前缀的对应节点，答案加上该结点的 $sum$

即对 $T$ 的每个前缀，把答案加上所有后缀在 $S$ 中的出现次数

每个点到根的 $size$ 之和，就是其所有后缀的出现次数

9-6

Process

T1的小结论我讲课讲过，积分部分也不难；T3是已经没有什么好害怕的了的弱化版。。。

T2题没看懂，写了个乱搞拿了20分

考场上T3搞了很久才想起来做法，反映出自己容斥还是比较弱，需要加强

T1

[积分] [概率和期望] [方差]

首先有

D(X) = E(X^2) - E^2(X)

后面显然就是 $(\frac{l+r}{2})^2$ ，前面可以积分，原函数是 $\displaystyle h(x) = \frac{1}{3}x^3 + C$ ，那么 $\displaystyle E(X^2) = \frac{\frac1 3x^3}{r - l}$

最后化简一下， $\displaystyle D(X) = \frac{(r - l)^2}{12}$

T2

插头dp

T3

[容斥] [动态规划] [斯特林数]

容斥，设 $f_i$ 为恰好违反 $i$ 次规则的方案数， $g_i$ 为至少违反 $i$ 次规则的方案数

\begin{aligned} &g_k = \sum_{i=k}^{n}\binom{i}{k}f_i\\ \Rightarrow &f_k = \sum_{i=k}^{n} (-1)^{i-k}\binom{i}{k}g_i \end{aligned}

然后考虑如何求 $g$

显然题目中的 $v$ 没有意义，把 $v$ 排序后就是一个 $n$ 的排列。于是转化为，求有多少个排列 $p$ ，至少有 $k$ 个位置满足 $p_i < i$

设 $dp_{i, j}$ 表示考虑到第 $i$ 位，有 $j$ 个位置满足限制（不考虑顺序）的方案数，那么 $g_i = dp_{n, i}\times\binom{n}{i}\times (n - i)!$

今天才搞懂容斥是怎么回事。。。

这里 $dp_{n, i}$ 表示的，有 $i$ 个限制的方案，指的是只保证这 $i$ 个限制一定满足，而其他的数完全不考虑如何填的方案数，它并没有什么实际意义。乘上 $\binom{n}{i}\times(n-i)!$ 之后才表示至少有 $i$ 个限制的方案数

而这里定义的，至少有 $i$ 个限制的方案数，也并不是真正意义上的至少。因为这里的至少是会算重的，否则 $f_i$ 为什么不等于 $g_{i + 1} - g_i$

正确的定义应该是，强制（钦定） $i$ 个条件满足的方案数，只有这样才能从根本上使计数更加方便

这个 $dp$ 转移很简单，若第 $i$ 个数满足限制，那么它能填前 $i-1$ 个数的某一个；又因为前面已经选了 $j-1$ 个数，所以它只有 $i-j$ 种选法

dp_{i, j} = dp_{i - 1, j} + (i - j)\times dp_{i - 1, j - 1}

注意到，把数组第二维翻转后就是第二类斯特林数的形式

多项式可以优化到 $O(n\log n)$

9-8

Process

T1几分钟写完，T2看错题，以为所有关键点都要在联通块中，浪费了很久时间

T3最后二十分钟rush出来了

T1

或的答案就是整个数组，与的答案就是每个长度为 $k$ 的区间

T2

[动态规划]

用总联通块数 减去 不满足条件的联通块数即可

对于每个点，统计以它作为联通块的最低点的方案

T3

[堆][贪心]

贪心枚举最右边到了哪一列，中间每一列至少选一个，最多选 $n$ 个，总共要选 $k$ 个

用一个小根堆随便维护一下

9-9

Process

T1搞了好久，矩阵快速幂推式子又推了半天！！！

然后剩下时间都在搞T2，写了一个退火乱搞只拿到了35分。考完之后发现T3是sb题

简单题还是做得太慢！！！

T1

[矩阵快速幂]

随便找规律/搞系数，矩阵快速幂优化

T2

[边双] [缩点] [背包] [动态规划] [计数]

显然先缩边双。一个直观的贪心是枚举每个点为根，然后每个点从父亲往它连边

但是这个做法很容易被hack掉

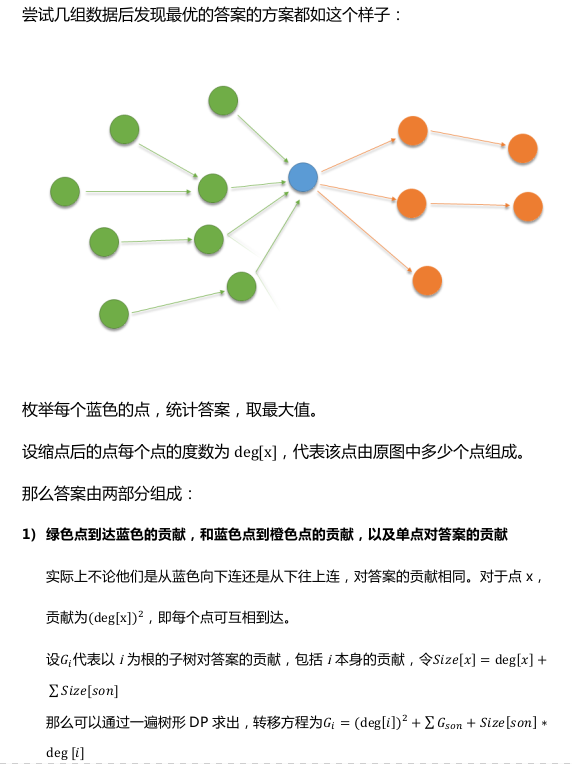
19-9-9-1

19-9-9-2

注意，题解中 $deg[i]$ 是表示 $i$ 这个边双的大小。。。

第一部分就是那个看成树的贪心，第二部分直接背包

T3

[set] [数据结构]

因为 $a_i\le 100$ ，于是考虑和值域相关的做法

对于每个权值维护一个set，存该权值的出现位置

每次枚举一个权值，求出其位于当前区间内的出现次数，然后删掉这一段

计算出平均值后，按照题意重新赋值

直接暴力搞肯定不行，发现每次赋值都是一些连续段，于是set维护pair，存这样的连续段即可

时间复杂度不太会分析，但是看上去很对，跑得也很快

9-10

Process

现在开始联考了，考场状态还是有点问题，要多锻炼

先写的T2，写了个 $O(nm)$ 的做法，随便找找规律就找出来了。T1暴力状压，复杂度 $O(3^nk^2)$ ，可以随便跑。T3考场上想了个 $O(n^3)$ 的背包，结果没调出来，应该是有问题的，因为不好组合

最后T3暴力还挂了分，很不应该

T1

[动态规划]

暴力状压

T2

找规律

T3

[概率和期望] [动态规划] [换根dp] [前缀和]

把题目中 $p^k$ 的贡献拆开，把 $p$ 拆到每个 $k$ 上

先枚举根，然后设 $f[i]$ 表示只考虑 $i$ 子树时的期望答案，因为 $i$ 的每个子树是独立的，所以可以直接把期望乘起来，再考虑 $i$ 这个点的影响。若在值域序列中， $i$ 插到最前面的位置（ $\frac{1}{size[i]}$ 的概率），则贡献 $p$ ；否则（ $\frac{size[x] - 1}{size[x] }$ 的概率）贡献 $1$

f[x] = \prod_{y\in son[x]} f[y] \times (\frac{p}{size[x]} + \frac{size[x] - 1}{size[x]})

然后换根 $dp$ 即可

因为 $\frac{p + size[x] - 1}{size[x]}$ 可能等于0，所以要记个前后缀积来dp

另外一种做法：考虑每个点的贡献，设 $sz[x]$ 表示在 $1$ 为根情况下的 $size$ ，则它的 $size$ 要么是 $sz$ ，要么是 $n-sz$ ，要么是 $n$

在 $dfn$ 上差分一下即可

9-12

Process

玩了好久的T1。T2考过。T3暴力没写完

Summary

不知道为什么还是感觉时间不够，又出现了暴力写不完的情况

感觉这几天有点集中不了精力去想题。。。

T1

先从大到小贪心，然后前十二位爆搜一下所有方案

T2

[对偶图]

平面图转对偶图，把原图中的面看成点

具体见此

T3

...

9-14

Process

三个比较规整的分，T2挂了20~30分，T3挂了20分

T1想得有点久，花了快半个小时的时间才想出来。T2搞了很久，因为没见过这个套路所以没搞出来。T3想了个假做法，写到一半才发现有问题

T1

[贪心]

从高位往低位贪心，每次看所有符合条件的边是否能使 $1$ 和 $n$ 连通

T2

[two pointers]

又是经典套路我不会系列

用两个栈维护队列，从而维护two pointers。这个东西常用于没有可减性的问题上

具体实现见此

T3

[kruskal重构树] [分块]

建kruskal重构树，对询问分块

9-18

Process

今天可能是这段时间以来唯一一次自己稍微满意一点的模拟赛了吧。。。

T1花了二十分钟，T2先写的 $O(n^3)$ ，然后优化到 $O(n^2)$ ，然后优化到了 $O(10n)$ 的。T3写了个暴力

没挂分，考试过程中比较虚，花了比较长时间检查，以至于T3没有太多时间思考

T1

[前缀和]

把坐标系旋转45度，然后直接前缀和

T2

[计数]

考虑枚举逆序对的位置 $(i, j)$ ，统计它对答案的贡献

暴力计算的时候需要枚举第一个没卡到上界的位置 $k$ ，分五种情况讨论

很容易用前缀和优化到 $O(n^2)$

再做一次前缀和，加上一点点非常简单的计数技巧就能优化到 $O(10n)$ 了

T3

[数据结构] [树状数组] [线段树] [set] [势能分析]

19-9-19-1

主要思想就是把询问离线，动态维护每个元素最右端位置，以统计答案

然后考虑链：给定的路径都是一段区间。也就是说，上述问题的每个元素变成了一段区间。

仍考虑上述做法，但需要支持快速把某一段区间的信息都更新

因为每次是整段整段地更新，每段内信息相同，于是考虑维护颜色段

直观的做法就是维护一个set，每次找到与当前 $[l, r]$ 相交的所有颜色段（包括包含），将它们暴力一个个删掉，再把当前段加入

复杂度简单势能分析即可

具体实现时，可以用线段树代替set，写起来更方便，没有细节。修改时要递归到只有一种颜色的区间（线段树维护min、max，判断min == max）

9-20

Process

先写的T2、T3，最后开的T1，T1写了很久，代码能力有点差。。。

T1

[树链剖分] [暴力]

注意到add数量很少，于是每次重构树剖即可

如果线段树维护的话，重构复杂度是 $O(n)$ （线段树build是 $O(n)$ ），询问 $O(\log^2n)$

ST表维护的话，重构复杂度 $O(n\log n)$ ，询问 $O(\log n)$

T2

[线性筛] [欧拉函数]

线性筛 $\varphi$ 即可

T3

[后缀自动机]

SAM随便算一下本质不同子串

9-21

Process

这场考得中规中矩，T3还有一些部分分可以拿到的，还是因为搞T2时间太长了，没时间写了

前两题没有挂分，希望以后也要保持

T1

[概率和期望]

根据期望的线性性，转化成求每个点期望之和。每个点期望就是 $\frac{1}{k!}$ ， $k$ 表示在它前面要经过多少个点才能到-1，树上算下深度即可

T2

[动态规划] [贪心]

设 $f[x]$ 表示从 $x$ 开始，需要多少体力才能不停顿地走完 $x$ 的子树（也就是把所有体力放到一开始加满）

设 $g[x]$ 表示 $x$ 子树中所有点权减两倍边权

树形dp，考虑从 $x$ 的儿子 $y$ 转移到 $x$

此时， $f[y]$ 就要先加上 $w_{x, y}$ ， $g[y]$ 要先减去 $2\cdot w_{x, y}$ （考虑当前这条边，以下的 $f$ 和 $g$ 均已进行完此操作）

不难发现，如果加满体力走完整棵子树的话，体力值会变化 $g[y]$

那么 $g[y] > 0$ 的儿子肯定要先遍历，且按照 $f[y]$ 从小到大遍历

$g[y] \le 0$ 的儿子后遍历，且按照 $g[y] + f[y]$ 从大到小遍历

按照这个顺序依次访问儿子即可

T3

前70分都比较可做，组合计数随便算算。满分做法需要复杂的分类讨论

9-23

Process

今天T1卡了好久的常，T2T3都没什么时间了

T2比较神仙，思路不是很容易想

T1

[模拟]

发现答案就是 $k$ 进制下的数位和模 $k$ 的值

$O(R - L)$ 暴力模拟进位即可

T2

[矩阵快速幂] [状态压缩]

把排列看成置换。因为每个数地位相等，可以转化成某个排列要变成单位置换（）

为什么要这么转化下面会讲

考虑在暴力的基础上优化，要把状态数量从 $n!$ 压下来：只记录本质不同的置换（只记录每种长度的轮换个数）

举个例子： $(2, 4, 5, 1, 3, 6)$ ，它有三个轮换分别是 $(2, 4, 1), (5, 3), (6)$ 。于是记录 $<1,2,3>$ 表示有大小为 $1, 2, 3$ 的轮换各一个

相当于是原来的一些本质相同的状态，被缩成了一个大状态

总状态数是整数分拆的方案数，只有 $150$ 左右

这样记录的话，处于同一个大状态中的每个小状态，它们的所有后继状态所处的大状态集合是相同的（好像有点绕）

并且，这样记录能够使终结点唯一地表示出来（ $n$ 个长度为 $1$ 的环是唯一的，这就是为什么一开始要转化）

于是就可以直接矩阵快速幂计算答案了

具体实现上稍微有点复杂

T3

[拓扑排序] [拆点]

sol from gc

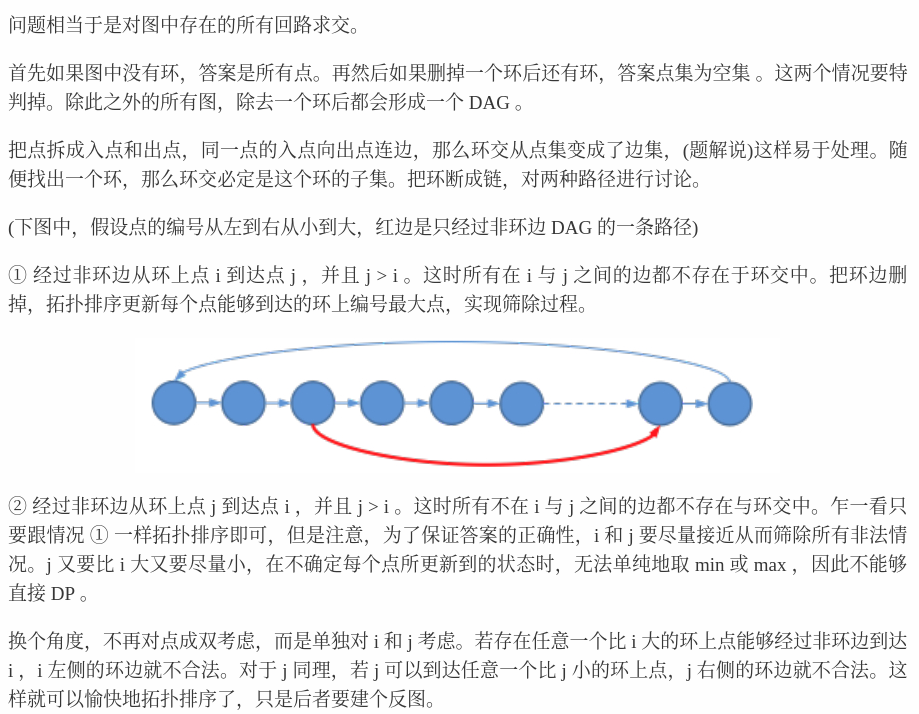
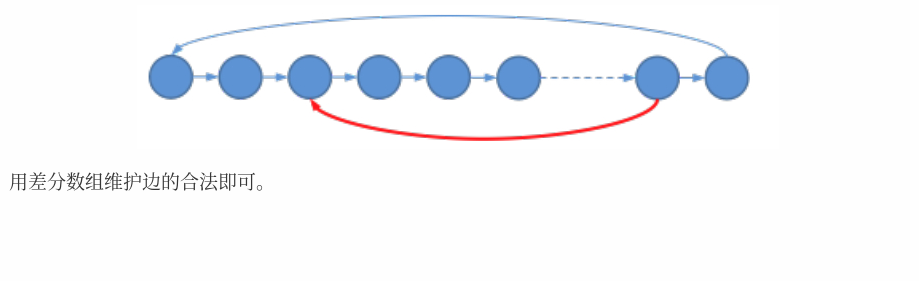
19-9-25-1

9-24

Process

T3以前见jwb做过，但是自己写的时候还是花了很长时间，最后只剩半个多小时写T1和T2了。

一开始花了很长时间看T1题意，但是又没写，浪费了较长时间，时间分配不合理，以后要注意

T1

[模拟]

化学题大模拟

T2

[动态规划] [贪心]

若给定的区间两两互不包含时是很好做的，因为排序后每次选的肯定是连续的一段

$dp[i][j]$ 表示到第 $i$ 个区间，分了 $j$ 组的答案，枚举下一段是从 $i+1$ 到 $j$ ，有转移

dp[i][k] + t_{a_i + 1} - s_{a_j} \rightarrow dp[j][k + 1] ~(t_{a_i + 1} > s_{a_j})

$s, t$ 是区间的左右端点

再考虑存在包含的情况

若 $A$ 含于 $B$ 中，则 $B$ 要么和 $A$ 放一组中，要么单独放一组

若 $B$ 和其他区间放一组，那把 $B$ 放到 $A$ 所在的组中， $A$ 组答案不变， $B$ 原来的组答案不会更劣

于是把只要包含了别的区间的区间单独提出来，贪心取较长的；剩下的区间做上述dp即可

最后再枚举两部分取的数目，把两部分合并起来即可

T3

[启发式分治]

先分解质因数，对每个位置求出，左边和右边第一个不与它互质的数的位置 $L_i, R_i$

这一步实现的时候要预处理每个数的最小质因子，否则时间很大

首先发现一个性质：若序列中的某个子区间不合法，则整个序列一定不合法

这个子区间无法被分隔开，最后一定会递归到这个区间上

于是可以每次利用 $L_i, R_i$ ，找出任意一个满足和其他数都互质的数作为根（ $O(1)$ 判断），再递归两边处理，伪代码如下：

19-9-25-4

但是这是 $O(n^2)$ 的

考虑启发式分治，即从两边同时向中间扩展：

19-9-25-5

这样复杂度就是 $O(n\log n)$ 的了，因为 $T(n) = T(x) + T(n - x) + O(\min \{x, n - x\})$ ，是启发式合并的逆过程

注意：从中间往两边搜是错的。因为只有从两边向中间搜才能保证搜到的点不在同一个区间中（左半边，右半边）

9-26

Process

两道原题，一道昨天才考过的题，不评价

T1

LOJ 3092

直接dp

T2

启发式分治即可

T3

[计算几何] [曼哈顿与切比雪夫距离]

首先找到所有交点：把线段按左边从小到大加入，统计它被哪些线段穿过即可

第二问直接曼哈顿转切比雪夫即可

对于第一问，设交点个数为 $k$ ，则

“对向交换”最多发生 $k$ 次，最少发生 $n - p$ 次。其中 $p$ 为“右边相对于左边的位置的排列的轮换数量”

比如，右边从下往上依次是 $3, 1, 2, 5, 4$ .那么轮换就是 $1\rightarrow 3\rightarrow 2,4\rightarrow 5$ .共两个

9-27

Process

状态不是很对，8:30之前一直没动键盘。T1想好久没想出来，T2也一直没想清楚

感觉今天静不下心来想题，要赶快调整状态了

T1

[生成函数] [卷积] [FWT]

设生成函数 $\displaystyle F_k(x) = \sum_{i} [a_i = k]x^i, G_k(x) = \sum_{i}[b_i=k]x^i$

那么在子集并卷积意义下，若 $[x^p]\displaystyle F_u * G_v \ge 1$ ，那么 $f[u][v]$ 就能对 $p$ 产生贡献

这样暴力每次把两个卷起来是 $O(n^32^n)$ 的，但是因为 $f[u][v]$ 也很小，所以先把每个DWT一下，把相同的 $f[u][v]$ 放一起加，最后在把每个 $H$ IDWT回去。大概是这个意思:

for (int i = 0; i < M; ++i) DWT (F[i], 1 << N, 0); 
for (int i = 0; i < M; ++i) DWT (G[i], 1 << N, 0);
for (int i = 0; i < M; ++i)
    for (int j = 0; j < M; ++j)
        for (int S = 0; S < 1 << N; ++S)
            H[f[i][j]] += F[i][S] * G[j][S];
for (int i = 0; i < M; ++i) DWT (H[i], 1 << N, 1);

复杂度 $O(n^22^n)$

T2

[启发式合并] [贪心] [set]

显然可以从叶子往上贪心。一开始把所有路径都加上，碰到不合法的点就把包含它且顶端深度最浅的路径删掉

包含它这个条件即为路径底端的点在它的子树内；可以在树上合并

深度最浅的条件可以用multiset维护

所以multiset启发式合并，动态维护可选路径集合即可

T3

...

9-30

Process

一道高考题，一道模拟题，一道原题

模拟题挂分挂得好惨。。。

T1

[赌徒破产问题] [特征方程] [数学]

2019年高考理科数学最后一题，只不过把数字换成了字母

随便推下式子特征方程搞下就可以了

T2

[模拟]

简单模拟题。用queue和list模拟即可。list是维护当前场上还剩下的人，以优化常数

T3

「GXOI / GZOI2019」旅行者