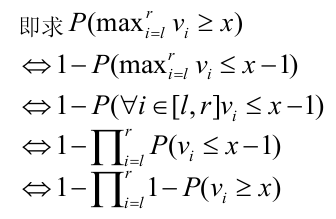2019年8月

搞颓记录

8-1

考了自己的题，结果T1锅了

T1 CF原题数据太水，导致我的假做法也能过

不过问题不太大，修改了一下就过了

8-2

Process

T1搞了一个小时，后面在想T2的20分怎么做，以及T3的正解做法，均无果

Score

100 + 10 + 30 = 140

T1

[数据结构] [线段树]

每个点维护一个二进制标记，如果第$i$位为$1$，则表示它子树内深度为$i$的点需要翻转左右儿子

修改的时候，因为至多只有首尾两层是不满的段，其他中间的段都是满的，因此中间的每次都是$O(1)$的，于是总复杂度是$O(n\log n)$的

修改不满的段的时候的做法比较巧妙，但也不难想，以后如果忘了看看代码就懂了。。。

T2

还没改，不知道会不会改

T3

[动态规划]

一个经典套路：忽略题意中的走的顺序，从左往右依次加点进行dp

那么原序列就会被分成若干个联通块(实际上是若干条链，这里暂且称作联通块)，设$dp[i][j]$为考虑到第$i$个点，有$j$个联通块的方案数，具体转移见代码

Code

inline int left (int x) { if (A[x] != 'R') return 1; return 0; }
inline int right (int x) { if (A[x] != 'L') return 1; return 0; }

// 这里的联通块是指一条链(方向不定，反正展开就是一条链)
// 需要保证每个联通块的末尾为R(因为前面的已经考虑过了，如果还剩了L就连不起来了)
// 普通联通块： 除了S所在联通块和T所在联通块，其他的联通块

// 每种点的作用：
// 能往左走： 连接前面两个联通块的桥梁; 作为某个联通块的开头
// 能往右走： 单独作为一个联通块; 作为某个联通块的结尾

inline void Solve ()
{
	memset(Dp, 0, sizeof Dp);
	if (A[N] == 'R' && T != N) { puts("0"); return ; }
	Dp[N][0] = 1;
	for (int x = N - 1; x >= 1; --x)
	{
		for (int k = 0; k <= N; ++k)
		{
			int &ans = Dp[x][k];
			if (x == S)
			{
				if (k && left (x)) Add (ans, (LL) k * Dp[x + 1][k - 1] % Mod);
				if (right (x)) Add (ans, Dp[x + 1][k]);
			}
			else if (x == T)
			{
				if (k) Add (ans, (LL) k * Dp[x + 1][k - 1] % Mod);
				Add (ans, Dp[x + 1][k]);
			}
			else
			{
				if (left (x))
				{
					if (k >= 2) Add (ans, (LL) k * (k - 1) % Mod * Dp[x + 1][k - 1] % Mod); // 连接两个普通联通块
					if (k && x > S) Add (ans, (LL) k * Dp[x + 1][k - 1] % Mod); // 连接普通联通块和首联通块
					if (x > T)
					{
						if (k) Add (ans, (LL) k * Dp[x + 1][k - 1] % Mod); // 连接普通联通块和尾联通块
						Add (ans, Dp[x + 1][k]); // 放在尾联通块的开头
					}

					Add (ans, (LL) k * Dp[x + 1][k] % Mod); // 放在普通联通块的开头
				}
				if (right (x))
				{
					Add (ans, Dp[x + 1][k + 1]); // 单独作为一个联通块
					if (x > S) Add (ans, Dp[x + 1][k]); // 放在首联通块的末尾
					Add (ans, (LL) k * Dp[x + 1][k] % Mod); // 放在普通联通块的末尾
				}
			}
		}
	}
	
	printf("%d\n", Dp[1][0]);
}

8-3

上午听zjm讲组合，生成函数，多项式；下午听zqc讲容斥反演

似乎迷迷糊糊听懂了一点，可是理解还是不够

8-4

Process

cxr的题，T1傻逼题居然没想到，自闭了自闭了

就写了T1 T3两个暴力，根本没开T2，后来改题的时候看T2发现好像也不太难

60 + 0 + 60 = 120

T1

真的是sb题

考虑把答案设为根，此时会有一些限制不满足，又因为一定在根的子树中，那么设$d_i$表示第$i$个限制至少需要深度$d_i$才满足限制，找到最大的$d_i$，以及其对应的点$x$，判断$x$是否合法即可

T2

[强连通分量] [缩点] [组合数学] [范德蒙德卷积]

题解很清楚

第二部分中，我们假设所有在$A$集合中的数都取到了最大值，显然它们还在$A$集合中，但相对位置可能会变化，不过对统计方案数并没有影响。

第二部分中$x$实际上还与$A$有关，即$cnt1 + x + 1 \le A$，因此不能直接把$\sum_{x}\binom{cnt2}{x}\binom{cnt1}{B-1-x}$利用范德蒙德卷积变成$\binom{cnt1 + cnt2}{B-1}$

T3

没改

8-5

Process

T3模板题， T1花了点时间推式子，T2傻逼dp居然都没想到（最后时间不太够，有点急）

100 + 30 + 100 = 230

T1

[数学]

设$a, b, c, d$分别为$(0, 0), (0, 1), (1, 0), (1, 1)$的数量

设$a_1, b_1, c_1, d_1$分别为这些状态在答案的左边的数量，$a_2, b_2, c_2, d_2$为右边

可以列出一些方程，手解一下就行

最后化出来一步$b_1 + c_1 = t$，那么取$b_1 = \min\{b, t\}$，看$c_1$是否合法即可

T2

[动态规划] [数据结构] [线段树] [单调栈]

设$dp[i]$表示取到第$i$个物品的答案，把与第几个箱子有关那个部分的贡献拆到后面去，即有转移：

$dp[i] = \min_{j}\{dp[j] + \max_{k=j + 1}^{i}\} + \sum_{j=i + 1}^{n}w_j$

单调栈 + 线段树维护一下$\max$部分即可

类似于19-6-22 T1

T3

[图论] [网络流] [欧拉回路]

混合图欧拉回路模板题

---

今天晚上想搞一点zjm课件的题

8-6

讲课，拖堂了1个小时

讲得有点累，幸好把话筒修好了，不然可能会当场去世

晚上把zjm的组合题搞完了

8-7

Process

今天整个不在状态。一个sbT2还想了一两个小时。

T1想了个乱搞，没搞出来。T3没怎么仔细想，结果爆零了

最后T2还因为没卡常爆成40

10 + 40 +0 = 50

T1

[动态规划] [搜索]

枚举每个点作为起点搜索 , 设 $dp[i][j][k]$ 为到 $(i,j)$ 吃到豆子的状态为 $k$ 的最大得分 .

如何记录是否吃到了某个豆子呢 ?

当蛇在豆子的右边穿过奇数次时就能包围住 , 穿过偶数次就没有包围住.

预处理一下经过某个点后，豆子是否被选中这个状态如何改变即可

T2\

[二分答案]

二分答案，差分check

这里必须要加一个优化：不要每次都从1到mid去算答案，而是类似于一个指针在上面移动，维护上次check到这次check中间的变化量

T3

[动态规划] [组合数学] [容斥]

不难发现，每行填的数都是一个排列去掉一个数

枚举这个断点即可得到$O(n^3)$的暴力，稍微优化一下就变成$O(n^2)$

设$dp[i][j]$表示第$i$行，断点在$j$的答案，则：

$dp[i][j] = dp[i - 1][j + 1] + dp[i][j - 1]$

结合这里的图可以发现，答案就是从原点出发，只能向右或向上走，不接触直线A,B，到达点$(n+m+1,n)$的路径条数

考虑容斥，先算从原点到$(n + m + 1, n)$的总方案数，减去碰到$A, B$的方案数

考虑将终点$p$关于$A$对称得到$p'$，发现从原点到$p'$的方案数就是碰到A至少一次的方案数

同理，关于$B$对称后的答案是碰到B至少一次的方案数

显然这样又会算重，算重的情况是先碰到A，然后碰到B，或者先碰到B，然后碰到A

也就是碰到边界的序列中存在AB或BA子序列的方案

于是又可以继续对称，把终点先关于$B$对称，再关于$A$对称，即算出了存在子序列AB的方案

以此类推

不难发现容斥系数为$(-1)^{cnt}$，$cnt$表示对称的次数

---

模拟求解即可，对称到不在第一象限时就停止。最多对称$\log$次

19.10.6 UPD

之前可能还是没太搞清楚

显然，总方案去掉经过$A$或$B$的方案就是答案

如何保证一种经过$A$？

把终点$p$关于$A$对称得到$p'$，起点到$p'$的方案数就是至少经过一次$A$的方案数。B同理

但这样算是错的，因为子序列$AB$会被$A$减一次，被$B$减一次，减了两次；$BA$同理

所以要加上经过子序列的情况（终点依次关于对称

但子序列$ABA$就没算了（被减一次，被加一次），必须要再减一次；$BAB$同理

注意，此时$ABB$并不会多算（被减一次，被$AB$加一次，刚好是$-1$）

以此类推

8-8

Process

T1花了半个小时，然后一直在搞T2。T2完全没有想到分治，一直在往扫描线的方向去想，始终无果

T1

见GC's Blog

T2

[分治]

统计序列中点对的问题要往分治上想！！！

考虑跨区间的贡献！！！

想到分治后不难

题解写得还可以

T3

[动态规划]

最后需要找到一个$t$，使得$\sum_{i=1}^{n}\_\_builtin\_popcount(t + mx - a[i])$最小

可以考虑$t$在每一位上的取值(0/1)，然后dp

暴力dp需要知道当前位往下一位有哪些数进了位

但是不难发现，若一个数前$i-1$位对应的数越大，它在第$i$位越容易进位

那么根据这个性质每次将数排序后，进位的数就是一段前缀了

具体细节可见Sol/Code

8-9

上午xz讲数据结构，下午jwb讲线段树

今天有点晕，不想接受新的东西。。。就水过去了

有时间搞下jwb的课件

8-10

Process

开场想了下T1，无果。然后发现T2很sb，写完之后去看T3，发现一个很直观很暴力的线段树合并做法。

T3调到考试结束前半个小时，最后慌慌张张写T1暴力，结果部分分写挂了

最后T2也挂了20分。。。

35 + 80 + 100 = 215

T1

[图论] [边双]

转化为求多少点对之间存在至少$d$条不相交路径

• 若联通：至少1条
• 若在同一个边双中：至少2条
• 若把图中任意一条边删除后，它们仍在同一边双中：3条

第三种情况枚举删哪条边即可

T2

转化为求的$(x, y)$对数，其中$yl$表示$y$的位数

枚举$x$，再枚举$yl$，用个$map$随便数下有多少个$y$即可

T3

[数据结构] [线段树] [线段树合并]

我的暴力线段树合并做法：

对于一个询问$x, k$来说，它要找$x$子树内，边权前缀$\max\le k$的点的个数（这里的前缀意思是它到$x$的这一段路径）

维护一个权值线段树，下标是边权离散化之后的值，权值是每个边权对应的答案和

显然子树的限制可以通过线段树合并来解决

而对于一条权值为$d$的边来说，它子树内所有$\le d$的边都要变成$d$（因为是前缀$\max$）

直接在线段树上区间查，区间置$0$（把点直接删掉）即可

---

晚上搞了TJOI2015旅游和xsy1599A

8-11

Process

倒序做题，T1写了个斜率优化（差不多又快忘光了。。。）

50 + 100 + 100 = 250

T1

[动态规划] [斜率优化]

有一个性质没挖掘出来：

• 若钦定某个点在最优策略里被选，那么策略与它的值没有关系

剩下的看sol吧

用分治优化dp，同时用上斜率优化

T2

[贪心] [最小生成树]

贪心最小生成树

每个点只往它当前这一列的相邻点，以及另一列离它最近的两个点连边即可

T3

随便dp一下，处理出每个点到根的最短路

---

晚上把AGC028D搞完了，然后发现斜率优化学得狗屎样的，重新学了下

8-12

上午的贪心好神啊。。。

下午图论听了一部分

今天的课件都要找时间搞了

晚上搞了NOI2019D1T1和「LNOI2014」LCA

8-13

Process

前两题搞完的时候是10:40，太慢了。。。T2写了半天

T3写了个暴力，搞链的分但是做法有点问题

T1

题解很清楚

我直接找的规律，规律很好找

T2

[数据结构]

我的做法和$k$有关，对每个点直接枚举其对应的$k$的具体的值，剩下的条件随便维护下即可

也可以CDQ分治，做到与$k$无关

T3

[动态规划] [组合数学]

在$a$到$b$的链上dp，设$dp[i][j]$表示考虑到链上第$i$个点，它在操作序列中位于第$j$个位置

每次把点往前面的方案里插即可

对组合数的理解的应用还要再深一点

8-14

Process

想了一上午T1，不会做，期间想了一个假做法，以及推了下T2的式子，太麻烦就弃了

于是爆零了

0 + 0 + 0 = 0

T1

离散化之后就可以考虑每个单位格子对答案的贡献！！！

怎么这么sb都想不到

我想的做法是$n^2$枚举两个点，以它们形成的矩形去算贡献，但是会有细节问题

考虑单位格子的话就不存在各种奇奇怪怪的问题了！！！

T2

[概率和期望] [线段树]

做法来自xcy

考虑$[L, R]$中的每个点对答案的贡献，发现是$w_i * E(i)$，$E(i)$表示$i$这个点期望要走多少次

设$\displaystyle a = \prod_{j=i}^{R}p_j$，那么有

$\begin{aligned} E(i) &= a + 2 \times(1-a)\cdot a + 3\times (1-a)^2 \cdot a + ...\\ &=\sum_{k=0}^{\infty}(k + 1)(1-a)^ka\\ &=\frac{1}{a} \end{aligned}$

于是答案就是$\displaystyle \sum_{i=L}^{R}\frac{w_i}{\prod_{j=i}^{R}p_j}$

线段树每个结点维护一下$\displaystyle \frac{w_i}{\prod_{j=i}^{R}p_j}$和$\displaystyle {\prod_{j=i}^{R}p_j}$即可

最后把$n$开到2的幂次，预处理出修改需要的值即可

T3

[LCT]

思路：

对每种权值维护一棵树，每个结点有黑白两种颜色，白色表示这个点是当前这种权值，黑色表示不是

那么答案就是所有操作之后，每个黑色联通块的$size^2$的和

用LCT维护即可

计算答案的时候先初始化一个全是黑点的树，离线处理每个颜色，处理完一个颜色反着改回去

类似于CDQ分治时清空BIT的方法

具体实现见此，或出题人sol

8-15

神仙讲课

晚上搞了两道gc的课件

8-16

Process

刚了一上午的T2

60 + 100 + 20 = 180

T1

[动态规划] [计数]

求整数分拆的方案数

先考虑两种dp

$f[i][j]$ : 大小为$i$的数，用不超过$j$的数拆分的方案数

转移考虑是否加上一个权值为$j$的数

$g[i][j]$ : 大小为$i$的数，用$j$个数拆分的方案数

转移考虑把当前所有数$+1$，或者新加一个值为$1$的数

注意到，$f$的第二维只与权值大小有关，$g$的第二维只与个数有关

又因为权值大于$\sqrt n$的数不会超过$\sqrt n$个，于是可以考虑把$f$和$g$的第二维都只枚举到$\sqrt n$

这里要把$g$的定义稍微改一下，要保证这$j$个数都$> \sqrt n$

令$m = \sqrt n$，则答案长这样

$ans = \sum_{i=0}^{n}\Big(\sum_{j=0}^{m}g[i][j]\Big) \times f[n - i][m]$

T2

定义计算括号序列为将$($看成$+1$，$)$看成$-1$，求前缀和

我的做法比较暴力

首先考虑把所有$?$先看成$($，计算括号序列的值，设其为$a$数组

若某个合法的括号序列以$i$为左端点，则右端点$j$需要满足，从$i$开始走到$j$的过程中，括号序列的值非负

形式化地说，需要满足$\displaystyle \min_{k = i}^{j}a_j - a_{i - 1} \ge 0$

显然，这个式子具有单调性，即合法的右端点一定在区间$[i, R_i]$中，可以二分求出$R_i$

---

同理，把$?$看成$)$，计算后缀括号序列后，也能类似地求出$L_i$，表示以$i$为右端点时，左端点一定在区间$[L_i, i]$中

一个小结论：只要满足$[i, R_i]$和$[L_i, i]$这两个限制，就一定能构造出合法地括号序列

考虑枚举右端点$i$，那么就是要找有多少个左端点$j\in[L_i, i]$，满足$R_j \ge i$

这个随便用个数据结构维护一下即可

T3

[线段树] [树链剖分]

8-17

gc的题，我验的题

T1

[组合数学]

补集转化，然后用插板法算下方案数即可

T2

[单调栈] [线段树]

先处理出关于$c_i$递减的单调栈

按$v_i$排序，从小到大考虑，在单调栈上二分找到恰好能卖的那个位置

从那个位置开始把一段前缀减掉，用线段树维护即可

T3

把点权拆到边权上，每次考虑一个点把之前的哪个点作为父亲最优

显然只要考虑它到原树的根的那条链上的点即可，因为其他点都不会更优

---

晚上打了百度之星初赛

T2贪心没搞出来，没进250。。。

8-18

上午csy讲字符串，有一两道题断了

下午xcy讲树，基本还在线

晚上打了百度之星初赛第二场

抄了GC的T4，最后排名77

8-19

Process

似乎现在在考的是去年纪中的题了

T1还没想清楚细节就开始码，导致浪费了很多时间，最后只能交个$\log^2$的暴力草草收场

T2考过很多次了，结果遇到的时候还话了不少时间才看出来是那个模型。。。

T3没时间了，暴力没调出来（实际上是看漏了个条件）

Summary

现在开始的模考一定要认真对待！！！

每道题先写好暴力，想正解/码正解的题一定要掐好时间，不能出现暴力分没写完，甚至是有题爆零的情况！！！

T1

改了个好多细节的做法

二分某一个数组的下标，那么可以计算出另外一个数组期望的下标

再通过判断两个数组某些位置上的值的大小关系判断往左还是往右走

T2

$dp[i] = \max_{j=0}^{i-1}dp[j] + f(\min _{k=j+1}^{i}a_k)$

和这天一模一样

T3

[概率和期望]

首先有一个式子：对于一个随机变量$x$，其期望值为$\displaystyle E(x)= \sum_{i=1}^{\infty}P(x\ge i)$

根据期望的线性性把式子拆开，考虑每个比$x$小的$i$对答案的贡献

接下来对每个询问$[l, r]$，考虑每个$x$的贡献：

也就是说，我们只需要求出$[l, r]$内每个位置的最小值$\ge x$的概率$\big(P(v_i\ge x)\big)$

它就是小于$x$的数不选的概率的乘积，减去所有数都不选的概率

---

然后考虑$x$在变化的时候，答案如何变化（假设从$y$变为$x$）

显然，最外面的1-可以最后计算，于是可以只考虑$\displaystyle \prod_{i=l}^{r}1 - P(v_i\ge x)$的变化，那么直接除掉$1 - P(v_i\ge y)$，再乘上$1 - P(v_i\ge x)$即可

但是这样做当$P(v_i\ge x) = 1$时会有问题，不过因为$P(v_i \ge x)$是随$x$的变大而递减的

即若$\exists x> y, P(v_i\ge x) = 1$，那么$P(v_i\ge y) = 1$

所以从大到小枚举$x$就行了

---

最后考虑多组询问如何处理

因为所给区间互不包含，所以每个点被包含的区间也是一个区间

只需要把答案的这段区间直接乘上当前的贡献，线段树维护即可

看代码可能更好理解。。。

Code

#include <bits/stdc++.h>

#define x first
#define y second
#define y1 Y1
#define y2 Y2
#define mp make_pair
#define pb push_back
#define DEBUG(x) cout << #x << " = " << x << endl;

using namespace std;

typedef long long LL;
typedef pair <int, int> pii;

template <typename T> inline int Chkmax (T &a, T b) { return a < b ? a = b, 1 : 0; }
template <typename T> inline int Chkmin (T &a, T b) { return a > b ? a = b, 1 : 0; }
template <typename T> inline T read ()
{
	T sum = 0, fl = 1; char ch = getchar();
	for (; !isdigit(ch); ch = getchar()) if (ch == '-') fl = -1;
	for (; isdigit(ch); ch = getchar()) sum = (sum << 3) + (sum << 1) + ch - '0';
	return sum * fl;
}

inline void proc_status ()
{
	ifstream t ("/proc/self/status");
	cerr << string (istreambuf_iterator <char> (t), istreambuf_iterator <char> ()) << endl;
}

const int Maxn = 2e5 + 100;
const int Mod = 1e9 + 7;

namespace MATH
{
	inline void Add (int &a, int b) { if ((a += b) >= Mod) a -= Mod; }

	inline int Pow (int a, int b)
	{
		int ans = 1;
		for (int i = b; i; i >>= 1, a = (LL) a * a % Mod) if (i & 1) ans = (LL) ans * a % Mod;
		return ans;
	}
}

using namespace MATH;

int N, M, Q;
struct info
{
	int x, y, p;
} A[Maxn];
pii B[Maxn];

stack <int> stk[Maxn];
int base[Maxn];
int L[Maxn], R[Maxn];

inline int cmp (info a, info b) { return a.y < b.y; }

inline int cmp_x (pii a, pii b) { return a.x < b.x; }

inline int cmp_y (pii a, pii b) { return a.y < b.y; }

namespace SEG
{
#define mid ((l + r) >> 1)
#define ls o << 1
#define rs o << 1 | 1
#define lson ls, l, mid
#define rson rs, mid + 1, r
	struct info
	{
		int sum, tag;
		info () { sum = 0, tag = 1; }
	} node[Maxn << 2];

	inline void push_up (int o) { node[o].sum = (node[ls].sum + node[rs].sum) % Mod; }
	
	inline void push_down (int o)
	{
		if (node[o].tag == 1) return ;
		node[ls].sum = (LL) node[ls].sum * node[o].tag % Mod;
		node[rs].sum = (LL) node[rs].sum * node[o].tag % Mod;
		node[ls].tag = (LL) node[ls].tag * node[o].tag % Mod;
		node[rs].tag = (LL) node[rs].tag * node[o].tag % Mod;
		node[o].tag = 1;
	}
	
	inline void build (int o, int l, int r)
	{
		if (l == r) return void (node[o].sum = 1);
		build (lson), build (rson);
		push_up (o);
	}
	
	inline void update (int o, int l, int r, int x, int y, int val)
	{
		if (x > y) return ;
		if (x <= l && r <= y)
		{
			node[o].sum = (LL) node[o].sum * val % Mod;
			node[o].tag = (LL) node[o].tag * val % Mod;
			return ;
		}
		push_down (o);
		if (x <= mid) update (lson, x, y, val);
		if (y > mid) update (rson, x, y, val);
		push_up (o);
	}
	
	inline int query () { return node[1].sum; }
#undef mid
}

inline void Calc (int x)
{
	int pre = 1 - (stk[x].top() - base[x]) % Mod + Mod;
	stk[x].pop();
	int now = 1 - (stk[x].top() - base[x]) % Mod + Mod;
	SEG :: update (1, 1, Q, L[x], R[x], (LL) now * Pow (pre, Mod - 2) % Mod);
}

inline void Init ()
{
	sort (A + 1, A + M + 1, cmp);
	for (int i = 1; i <= N; ++i) stk[i].push (1);
	for (int i = 1; i <= M; ++i)
	{
		int res = stk[A[i].x].top();
		stk[A[i].x].push ((LL) res * (1 - A[i].p + Mod) % Mod);
	}
	for (int i = 1; i <= N; ++i) base[i] = stk[i].top();

	sort (B + 1, B + Q + 1);
	for (int i = 1; i <= N; ++i)
	{
		L[i] = lower_bound (B + 1, B + Q + 1, mp (0, i), cmp_y) - B;
		R[i] = upper_bound (B + 1, B + Q + 1, mp (i, 0), cmp_x) - B - 1;
	}
	
	SEG :: build (1, 1, Q);
}

inline void Solve ()
{
	Init ();

	int ans = 0, i = M;
	while (i)
	{
		int j = i;
		while (A[j].y == A[i].y && j >= 1) Calc (A[j].x), --j;
		Add (ans, (LL) SEG :: query () * (A[i].y - A[j].y) % Mod);
		i = j;
	}
	
	ans = ((LL) Q * A[M].y % Mod - ans + Mod) % Mod;
	cout << ans << endl;
}

inline void Input ()
{
	N = read<int>(), M = read<int>(), Q = read<int>();
	for (int i = 1; i <= M; ++i)
		A[i].x = read<int>(), A[i].y = read<int>(), A[i].p = read<int>();
	for (int i = 1; i <= Q; ++i) B[i].x = read<int>(), B[i].y = read<int>();
}

int main()
{

	freopen("max.in", "r", stdin);
	freopen("max.out", "w", stdout);
	
	Input ();
	Solve ();
	
	return 0;
}

8-20

Process

又看错题。。。T2算方案数的时候看成当且仅当$a_i$不同，死活不会算

T1想错了一个地方，以为$m$只会到$10^6$。。。

T3比较简单，直接矩阵快速幂即可

T1

[贪心] [动态规划]

显然对于相同体积的物品只用留权值最大的

暴力是$O(100m)$，考虑$m$比较大的时候直接取性价比最高的，当$m$到$10^6$左右的时候再dp

T2

[卡特兰数]

第一问用后半部分减去前半部分

第二问奇偶部分相减

第三问括号序列，直接卡特兰数

T3

[容斥] [矩阵快速幂]

暴力容斥，然后矩阵快速幂算方案数

8-21

上午sxy讲课，又复习了下往年联赛题

下午自己在搞xcy课件

8-22

Process

刚了一上午T2，就没时间了

T1

[组合数学] [容斥]

把$n$拆成两部分，一部分是若干个$m$，另一部分是用$k$个$[1, m-1]$的数凑出剩下的部分

设第一部分为$im$，那么剩下的就是$n-im$

因为$k$个$[1, m-1]$能凑出的数在$[k, k(m-1)]$范围内，因此$n-im\in[k, k(m-1)]$，这个范围是很小的

于是就可以枚举所有$i$了

第一部分可以直接插板法算，是$\displaystyle \binom{i + k - 1}{k - 1}$

第二部分需要容斥，枚举有多少个数不合法（大于$m-1$），是$\displaystyle \sum_{i=0}^{k}(-1)^i\binom{k}{i}\binom{(n-im)-i(m-1)-1}{k-1}$

T2

[点分治]

点分治，然后数点

看上去需要二维数点，但是可以通过把某一维排序后降到一维

排序后不一定保证数出来的点分属两个不同的子树，于是需要把每个子树的答案减去

这应该是点分治的一个经典技巧，大概是这个意思：

Add (ans, process (x, A[x], A[x]));

for (int i = Begin[x]; i; i = Next[i])
{
    int y = To[i];
    if (Vis[y]) continue;
    Add (ans, Mod - process (y, A[x], A[x]));
    divide (y);
}

T3

[毒瘤]

不是sol的做法

考虑询问的$x$和$y$的中点$mid$（假设$mid$在$x$到$lca$的链上）

答案由几部分取max构成：

• $lca$子树外的最长链

• $lca$子树内除了$x$和$y$所在子树，剩下部分的最长链

• $x, y$子树最长链

• 设$lack[i]$表示$fa[i]$的所有子链中，除了$i$所在的链外，最长的子链

  $x$到$mid$路径上，找到一个最大的$i$，满足$lack[i] + dis(fa[i], x)$最大

  $y$到$lca$路径上，找到一个最大的$i$，满足$lack[i] + dis(fa[i], y)$最大

• $mid$到$lca$路径上，找到一个最大的$i$，满足$lack[i] + dis(fa[i], y)$最大

前面三种情况随便处理

第四种情况把$dis$拆开，就是要使$lack[i] - dep[fa[i]]$最大，倍增即可

第五种情况同理

剩下就是一些细节

8-23

Process

T1写了一早上，结果看错题了，是个分块模板题

后面又没时间搞了

T1

[分块]

直接分块，暴力维护答案，搞个tag就可以了

T2

$f$是个积性函数，然后直接按题解那个式子筛就可以了

T3

[概率和期望] [动态规划] [矩阵快速幂]

好神仙的概率期望

• 为什么要处理一个$b$数组？

  因为当当前格子填$1$的话，它右边的那个格子就只能填$2$，否则会合并

最难理解的地方是dp转移分母那里

和贝叶斯长得很像，但是感觉还是没完全理解。。。

8-25

Process

T1就是暴力，随便写了下

T2猜结论，推了下性质搞出来了

后面由于某些特殊原因没怎么搞了

T1

暴力

T2

sol写得挺好

观察性质，猜结论，转化成坐标系中的经典问题

T3

sol写得挺好，看subtask3和subtask6

8-26

Process

搞了一上午T3，搞出来了，T2暴力写挂了

T1

若后手存在两个王，则先手胜，否则后手胜

T2

[分治]

因为操作可逆，显然可以把$A, B$排序

考虑归并排序，然后考虑如何把两个已经排好序的区间合并

假设考虑到$[l, mid]$和$[mid + 1, r]$

那么从$mid$开始往左找到一个最大的$x$，满足$A[mid - x + 1] > A[mid + x]$

然后把$[mid - x + 1, mid],[mid + 1, mid + x],[mid - x + 1, mid + x]$依次翻转，因为它们都是有序的

那么此时$[l, mid]$都比$[mid + 1, r]$小了，递归处理$[l, mid]$以及$[mid + 1, r]$即可

T3

[动态规划] [计数]

考虑一个个往后填颜色，设$f[i][j][k]$表示到第$i$位，前面已经出现了$j$种颜色，这$j$种颜色中有$k$种颜色在后面还可以

这是类似于一个栈一样的东西

比如如果填了1 2 3 4 3，那后面就不能填4了

可以先钦定一个排列顺序，最后乘上排列数

$f[i][j][k]\rightarrow f[i + 1][j + 1][k + 1]$

$f[i][j][k] \rightarrow f[i + 1][j][l], l\in [0, k]$

填表法，那么第二个转移就是一段后缀了

这是$O(nm^2)$的做法，考虑优化

发现$n$比$m$大了很多，会出现很多相邻的，颜色相同的点，考虑把这些点缩成一块考虑

按题意的方法刷颜色的话，每次最多只会增加两块，也就是块的个数最多为$2m-1$

于是第一维只要枚举到$2m-1$，再用插板法算下方案数即可

8-27

听了一些神仙题

要抓紧时间写完

8-28

Process

先搞了T2，然后写了T1，最后T3没调出来交了一个错的优化，结果获得了90分的好成绩

T1

[动态规划]

$f[x][i]$表示从$x$开始走，走$i$步，不一定回到自己的答案

$g[x][i]$表示从$x$开始走，走$i$步，一定回到自己的答案

树上背包转移

T2

[分块]

以$k$为块大小分块，每个询问区间只会落在相邻的两个块中

T3

[two pointers] [set]

固定左端点$i$时，右端点$j$是单峰的。即若$\min_{x, y\in [i, j]}|a_x - b_y| > j - i + 1$，往右移右端点会更优，否则往左移

会更优

two pointers即可

需要用set维护那个min，一个维护当前状态，一个维护差值。这是个很经典的套路

一开始加入左右inf，可以简化代码细节

8-29

Process

T1开场写了，T3想了个超级复杂的做法，搞了一上午搞出来了，T2暴力

T1

参见noip2018D1T1

T2

[动态规划] [计数]

发现$< n^m$和$>n^m$的方案数是相同的，因为任意一个$<n^m$的方案，把每个数用$n$除掉之后，一定都能得到一个合法的，$>n^m$的方案

于是只需要计算$=n^m$的方案

$n$的每个因子独立，拆开分别dp算一下再乘起来即可

具体转移看sol

T3

[概率和期望] [高斯消元] [换根DP]

我的做法：

考虑一个类似PKUWC随机游走的做法，设$f[i]$表示$i$的答案，根据树上高消的套路可以表示成$f[x] = A[x]\cdot f[fa[x]] + B[x]$的形式

容易想到可以直接用线段树维护这个东西

但是对于不同的询问，每次$A[x] = B[x] = 0$的点不一样

于是把询问离线，把询问挂在$y$上。一边dfs整棵树，一边处理询问

这样的话每次换根就只会有两个点的系数发生改变

---

正解：

考虑每条边的贡献（即这条边产生贡献的期望时间）

设$f[i]$表示$i\rightarrow fa[i]$这条边的贡献，$g[i]$表示$fa[i] \rightarrow i$这条边产生的贡献

显然，$f[i] = \frac{1}{deg_i} + \frac{1}{deg_i}\sum_{j}(1 + f[j] + f[i])$

化简得到，$f[i] = 2\cdot size_i - 1$，$g[i]$同理

然后随便搞下就可以了