Atcoder

[Atcoder]

sb题

ARC

090

F

Solution

[暴力]

分类讨论

1. $f(l) \le 7$：暴力

2. $f(l) \ge 8$：显然$f(r) - f(l) \le 1$，且区间长度一定会$\le \lfloor \frac{S}{8}\rfloor$，于是考虑枚举区间长度$len$

   • $f(r) - f(l) = 0$：方案数为$10^{\frac{S}{len}} - 10^{\frac{S}{len} - 1}- len + 1$

   • $f(r) - f(l) = 1$:

     设有$x$个数长度为$f(l)$，$y$个数长度为$f(r)$，那么有

     于是对于每个$len$，都能解出唯一确定的解

     需要注意当$f(l) | S$时答案在前一种情况中计算过了

Code

Summary

• 小范围暴力，缩紧条件以方便计数

091

E

[Dilworth定理]

猜了个结论，贪心构造方案，没想到就A了

根据Dilworth定理：最小链覆盖等于最长反链，即最长下降子序列的长度等于极长上升子序列的个数

那么可以类似这样去构造：$(7, 8, 9 , 10), (5, 6), (3, 4), (2), (1)$

这个例子中，$LIS = 4,LCS = 5$

092

E

为什么sb题又做不出

可能一定程度上是被这数据范围误导了吧，明明是线性做法

首先观察到对答案有贡献的位置的奇偶性是相同的

那么答案要么是所有奇数位上大于零的数之和，要么是所有偶数位上大于零的数之和

选一个较大的即可

F

[强连通分量]

考虑一条边$(a, b)$

• 若$a, b$在同一个强连通分量中：

  那么$b$能到达$a$

  若$a$能只通过这条边到$b$，则反向后答案改变，否则不改变

• 若$a,b$不在同一个强连通分量中：

  那么$b$不能到达$a$

  若$a$还有另一条路径能到达$b$，则答案改变，否则不改变

考虑如何判断是否存在另外一条路径能到达$b$

枚举$a$，考虑$a$的所有出边指向的节点

按的顺序dfs一次

假设从$b_i$开始dfs，访问到某个节点的时候，如果它没有标记，则标记上$i$，否则退出

再按同样的方法的顺序dfs一次

这样就能对每个点求出，经过它所需的编号最小的出边，以及编号最大的出边了

若二者相等，则只有这一条出边能到达这个点

复杂度是$O(nm)$的，能跑过

093

E

[最小生成树] [计数]

这道题居然自己做出来了！！！

好开心！

容易发现一个结论

• 最终答案的MST方案，与原图的任意一一种MST方案相比，最多只能有一条边的差别

若有两条有差别的话，那么一条染白，一条染黑，一定合法且更优

然后就基本做出来了

设$sum$表示原图的MST答案，讨论一下三种情况：

• $sum > X$：无解

• $sum = X$：

  一开始答案是$2 ^ m - 2 * 2^{m - (n - 1)}$

  至少一条边颜色不一样，就是总数减全黑或全白

  枚举其他的每条边，强制其在MST中，然后做最小生成树。

  若有$k$条边$=X$，则答案要加上$2 * \Big(2^{m - (n - 1) }- 2^{m - (n - 1) - k}\Big)$

  先确定原图MST方案那些边的颜色$p$，然后从$k$条边中至少选一条与$p$颜色不同，剩下的随便选的方案数

• $sum < X$：

  设有$prob$条边，满足答案为$X$，有$ban$条边，满足答案$< X$

  与上一种情况考虑类似，先确定原图MST方案那些边的颜色$p$，然后从$prob$条边中至少选一条与$p$颜色不同，且剩下的边中有$ban$条边也要与$p$颜色相同的方案数

  即$2 * \Big(2^{m - (n - 1) - ban} - 2 ^ {m - (n - 1) - ban - prob}\Big)$

F

Description

有 $2^n$ 名选手，编号为 $1$ 至 $2^n$ 。现在这 $2^n$名选手将进行 $n$ 轮淘汰赛，决出胜者。若 $x<y$，则 $x$ 能够战胜 $y$ 。但有 $m$ 个例外，$1$ 号选手会输给这 $m$ 个选手。问有多少中排列方式使得 $1$ 号选手取得胜利。

$n, m\le 16$

Solution

[容斥] [动态规划]

算是这几天学习容斥的小练习题，但是还是看了题解。。。

记 $m$ 个例外形成的集合为 $A$ 集合

首先可以固定$1$号选手在$1$的位置（最后乘$2^n$），那么题目就转化为，使得$\{p_2\},\{p_3,p_4\},\{p_5, p_6, p_7, p_8\}\cdots$这$n$个区间的最小值不能在$A$集合中

显然可以容斥，因为$n$很小，可以对这$n$个区间的限制，枚举所有情况暴力容斥

$\displaystyle ans = \sum_{S}(-1)^{S}f_S$，其中$f_S$表示强制$S$集合的区间的最小值在$A$集合中的方案数

因为这里枚举了所有情况，所以不需要乘组合数。。。

然后考虑求$f_S$

与这道题类似的套路，把$A$集合从大到小排序，设$dp[i][S]$表示考虑到$A$集合中的第$i$个元素，强制$S$集合的区间的最小值在$A$集合中的方案数

转移就是枚举第$i$个数出现在第$j$个区间中（也可以不出现），再从剩下可选的数中挑$2^j - 1$个数出来

因为是从大到小考虑的，所以剩下可选的数很好计算

Code

int ALL = (1 << N) - 1;
Dp[0][0] = 1;
for (int i = 0; i < M; ++i)
	for (int S = 0; S <= ALL; ++S)
	{
		if (!Dp[i][S]) continue;
		Add (Dp[i + 1][S], Dp[i][S]);
		for (int j = 0; j < N; ++j)
		{
			if (S & pw[j]) continue;
			int coef = (LL) C (pw[N] - S - A[i + 1], pw[j] - 1) * fac[pw[j]] % Mod;
			Add (Dp[i + 1][S | pw[j]], (LL) Dp[i][S] * coef % Mod);
		}
	}

• 为什么阶乘要乘在里面，而不能最后乘？

  因为你挑了某一些数之后，它们就只能在内部排列了

AGC

028

A

答案要么是$-1$，要么是$\mathrm{lcm}(n, m)$

B

[概率和期望]

连个B都做不出来。。。

先把答案转化为总方案数乘每个数贡献的期望

对于第$i$个数，它产生贡献的概率是$\sum_{j=1}^{n}\frac{1}{|i - j| + 1}$

这个概率的套路和这道题)几乎一模一样。。。

处理下逆元的前缀和即可

Summary

• 对整体算所有情况的答案时可以转化为求概率期望

C

[构造]

其实大体自己都想到了。一个小细节上想歪了，一直卡在那个细节那里就去看了题解。看了题解之后发现我是sb

发现一个合法方案中总共可能有这四类点：00, 01, 10, 11 （左边为$A_i$，右边$B_i$，$1$表示答案中有这个权值）

通过手玩发现，合法方案中00的个数与11的个数相等。并且只要满足$num_{00} = num_{11} > 0$，方案就一定合法

可以通过画图的方法来证明，并构造出方案

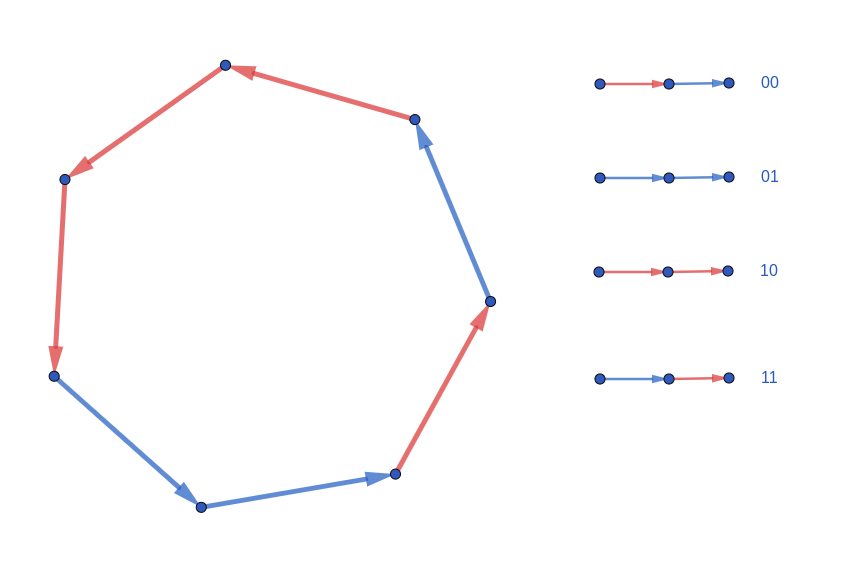
其中红色边为$A_i$，蓝色边为$B_i$

显然，红蓝两色分界处对应00和11，只要它们数量相等，那么其他类型的点分配在每条相同颜色边构成的链上即可

到这里其实都想到了。。。

当时感觉这样构造出来的方案有可能不可行，不过没关系，如果不可行那答案一定会比它更优

这样做只要能保证答案的情况能被算进来就行了

---

接下来就很简单了，把$A_i, B_i$混在一起排序，枚举00类的点是哪个（至少要一个），剩下的贪心选即可

记得考虑全是01或者全是10的情况

D

[计数] [动态规划]

转化一下

数轴上有一些点，已经存在的$K$条线段把数轴分成了一些部分

可以求出如果在任意两个部分之间连一条边，答案会增加多少

狗屎

看错题了，题目联通是指两个点通过某些线段联通，我以为把圆分成了多少个部分。。。

好难的计数题。。。

题解看了好久才懂

考虑最终状态，一定是某些编号连续的块（不一定是联通块）构成的

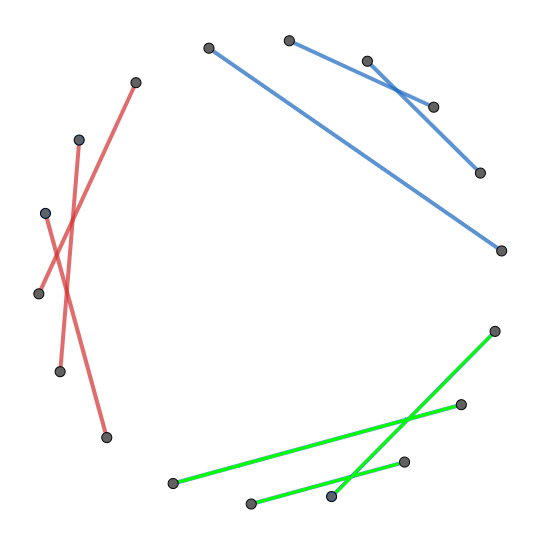
注：如图中的蓝色部分，它不是一个联通块，但这并不影响

考虑枚举所有这样的块，设$dp[i][j]$表示这样的块编号最小的点为$i$，最大的点为$j$，那么答案就是所有$dp[i][j]$乘上剩下点随便连的方案数

这样的块本质上就是满足$i$和$j$联通，且$i$到$j$之间的点只在内部互相配对

设$g[i]$表示$i$个点随便连边的方案数，若$i$为奇数，则$g[i] = 0$；否则$g[i] = (i-1) \times (i-3) \times \cdots \times 1$

如何计算$dp[i][j]$呢？

直接算并不好算，因为有图中蓝色块的情况，于是考虑简单容斥（补集转化），用所有方案减去$i$和$j$不联通的方案（枚举断点位置，相当于区间dp）

$dp[i][j] = g[cnt_{i, j}] - \sum_{k=i}^{j-1}dp[i][k]\times g[cnt_{k+1, j}]$

其中$cnt_{i, j}$表示$i$到$j$中没被钦定的点的个数

答案就是

$\sum_{i, j} dp[i][j]\times g[cnt_{1, i-1} + cnt_{i + 1, n}]$

029

A

显然答案就是每个$W$前面$B$的个数

B

贪心题。。。

不会做。。。

没脑子。。。

从大到小考虑，对于一个数$x$，找到它在剩下的数中能与它配对的数$y$，那么$y$是唯一确定的

设$y$是最小的满足$x + y = 2^k$的数，那么显然找不到一个$z > y$，满足 $x + z = 2^{k'}$

因为剩下的数中没有比$x$大的数，而这里的$z$肯定要比$x$大

于是可以直接将$x, y$配对

C

二分答案，判断的时候若$a_i > a_{i - 1}$就填0，否则把大于$a_i$位的部分删掉，再+1，用map暴力维护这个过程即可

D

这个D比较简单。。。

• 先手每次都必须往下走，不能停在原地
• 最后一定是停在某个障碍的上方，或地图最底下
• 后手在第$i$行时若最右能走到$p$的位置，那么第$i +1$行的$1$至$p$列若有障碍，则结束

030

A

sbt

B

手玩一下发现最优解是从$0$开始，先往左/右走一段距离，然后再反复横跳

枚举断点，预处理前后缀和计算答案