2019年7月

搞颓记录

7-12

三道题都不难。。。

T2小细节挂了20分

T3考场上居然不会十进制下的矩阵快速幂。。。

100 + 80 + 80 = 260

T1

完全背包

T2

[换根DP]

换根DP，处理下每个点上去和下去的最长链即可

T3

[矩阵快速幂]

递推式可以通过爆搜/找规律等方法求出，但是直接高精度+矩阵快速幂会T

考虑十进制下的矩阵快速幂

假设需要求$A^{1283}$，那么显然可以拆成$(A^1 * A^{1000}) * (A^2 * A^{100}) * (A^8 * A^{10}) * (A^3 * A^1)$

但显然$A^{10^{40000}}$不能快速求出，于是考虑优化。

$\Bigg(\Big(\big((A^1)^{10}*A^2\big)^{10} * A^8\Big)^{10} * A^{3}\Bigg)^{10}$

和读入优化类似的技巧：

sum = (sum << 3) + (sum << 1) + ch - '0';

把运算法则都升一级后显然也成立，也就是$A^{10} = \Big(\big(A^2\big)^2\Big)^2 * A^2$

复杂度就降下来了

7-13

今天崩了，11:20才做出来T1，后面两题都没看

正解想不出来的时候考虑暴力做法，一步步往下推就能推出来了

100 + 0 + 0 = 100

Process

T1

$dp[i]$表示从合成出$i$级武器开始，到合成出$n$级武器所需的期望花费

好像不能这么设。。。

$dp[i]$表示合成出$i$级武器的期望花费

令$\displaystyle a_i = \frac{\min\{c_i, b_{max\{0, i - 1\}}\}}{c_i}$

以下是错误思路。。。

$(dp[i - 2] + dp[i - 1])$有$a_{i-1}$的概率转移到$dp[i]$

$(dp[i] + dp[i + 1])$有$(1-a_{i+1})$的概率转移到$dp[i]$

$dp[i] = \frac{a_{i-1}}{a_{i-1} - a_{i+1} + 1}\times(dp[i - 2] + dp[i - 1]) + \frac{1 - a_{i+1}}{a_{i-1} - a_{i + 1} + 1}\times (dp[i] + dp[i + 1])$

边界：

$dp[0] = a$

$dp[1] =$

现在是10:47，我还一分都不会写。。。

状态设得可能有点问题，应该是第一次合成出$i$级武器的期望花费

考虑$dp[1]$，显然只要没合成出$1$级武器，就一直在$0$级不断合成，好像实际上不需要考虑$dp[2]$对它的影响

$\begin{aligned} dp[1] &= \sum_{i=0}^{\infty}(1-a_0)^ia_0\times (i+2)dp[0]\\ (1-a_0)dp[1] &= \sum_{i=1}^{\infty}(1-a_0)^ia_0\times(i+1)dp[0]\\ a_0\times dp[1] &= 2a_0\times dp[0] + \sum_{i=1}^{\infty}(1-a_0)^ia_0\times dp[0]\\ a_0\times dp[1] &= 2a_0\times dp[0] + (1-a_0)\Big(1-(1-a_0)^{\infty}\Big)dp[0]\\ a_0\times dp[1] &= 2a_0\times dp[0] + (1-a_0)\times dp[0]\\ dp[1] &= (1 + \frac{1}{a_0}) dp[0] \end{aligned}$

好像这样就过了样例了...

那么对于后面的dp值同理，应该也只需要考虑从前推过去的情况

$\begin{aligned} dp[n] &= \sum_{i=0}^{\infty}(1-a_{n-1})^ia_{n-1}\times \Big((i+1)dp[n-1] + dp[n - 2]\Big)\\ dp[n] &= \frac{1}{a_{n-1}}dp[n - 1] + dp[n - 2] \end{aligned}$

写的时候把$\frac{1}{a_n}$变成$a_n$

11:18终于签上到了。。。

T3

启发式合并维护倍增数组，$O(n\log^2(n))$

写不完了。。。

T1

[概率和期望]

process里讲完了

T2

数论，没碰

T3

[启发式合并] [倍增]

考虑启发式合并维护倍增数组

既然要启发式合并，那么树就必须要是一棵无根树，但原题因为要判断祖孙关系，必须要是一棵有根树

为了解决这个问题，只需要倍增时多维护一下边的方向即可，查询的时候要保证$x\rightarrow y$的路径上边的方向都相同且朝向$y$

7-14

Process

T1搞了好久，后面两道题没什么思路

100 + 20 + 52 = 172

T1

操作顺序对答案无影响

先全部操作列，考虑列对行的贡献，再操作行

T2

倍增？

复杂度太高了。。。

T3

$[l, r]$的答案：左端点$\in[1, l]$，右端点$\in[r, n]$的长度最小的合法区间

类似于二维数点？

T1

略

T2

[分块] [神仙题]

神仙题

首先显然会有循环，循环节是$m$的倍数，且大小$\le n * m$

暴力做法是每次$O(n*m)$找循环节，考虑一个类似于分块的优化：

记$jump[i]$表示第一列第$i$行走$m$步到达的位置，即每$m$步一大步，一大步一大步地走

再考虑修改操作：

假设修改$(x, y)$，那么只有可能$(x - 1, y - 1), (x, y - 1)(x + 1, y - 1)$这三个格子的决策发生变化，然后对第一列的某些格子的$jump$值产生影响

即我们需要考虑，第一列有哪些格子能走到当前格子

不难发现，它一定是连续的一段

因为上下两条曲线会将中间一块区域围起来，只要碰到边界就会走向目标格子

于是直接每次暴力往前找出连续区间的上下边界，修改其$jump$值

这个地方有不少细节，具体见代码。最主要的一个性质：

• 在往前推区间范围时，合法的上下界每次最多会往里缩小$1$

T3

Description

给定一个排列 P ，定义区间 [l, r] 是优美的当且仅当其中的数字在从小到大排列后是连续的，m 次询问，每次给定 [l, r] ，求包含它的最短优美区间。

$n, m \le 10^{5}$

Solution

[扫描线] [堆] [数据结构] [线段树]

扫描线 + 堆 + 线段树

其中线段树维护的部分非常厉害

一开始在线段树中对不同的节点赋不同的初值，巧妙地解决了，在扫描线移动时，后缀的长度同时发生变化的问题。即通过这种方法使得所有位置平等：离扫描线越远，初始赋上的权值越大

下面是具体做法

---

性质 1 ：定义 $p_{i}$ 为 i 在序列中的下标，$k_{i}$ 初始值为 i ，令指针 i 从前往后扫，每走一步，如果 $p_{v_{i}+1} < i$ ，就把 $[1,p_{v_{i}+1}]$ 的 k 值加上 1 ；如果 $p_{v_{i}-1}<i$ ，就把 $[1, p_{v_{i}-1}]$ 的 k 值加上 1 。这样操作之后，区间 [x, i] 是优美的当且仅当 $k_{x} = i$ 。

证明：若区间 [x, i] 是优美区间，设区间内元素排序后为 l...r ，那么对于 $i\in[l,r)$ 的每一对 i 和 i + 1 ，两者之中 p 较大的那一个都会让 $k_{x}$ 加 1 ，共加 i - x - 1 次，最终使 $k_{x}=i$ 。若区间 [x, i] 不是优美区间，$k_{x}$ 不可能加到 i - x - 1 次。

性质 2 ：包含某区间的最短优美区间一定是所有包含它的区间中右端点最左的一个。

反证：令 A 为一个这样的区间，如果 A 不最短，则 A 与答案区间 B 有相交部分，而且相交部分 C 必然是优美的，因为不可能有一个使 C 变优美所必需的数同时出现在 A, B 的非交部分内。那么这个 C 显然会更优，而且 C 的右端点同样最左。

综上，把询问挂在区间右端点上，扫描线 i 从前往后扫，每扫到一个询问就把它丢进优先队列里，队列内按左端点从右到左排序。同时用一棵线段树对 $r\in[1,i]$ 维护区间 [1, r] 中 k 的最大值，对于队首的询问区间 [l, r] 而言，若 $k_{j}, j \in [1,l]$ 最大为 i ，直接计算答案并永久弹出队列，然后继续 check 队首，如果不是，停止弹出。因为剩下的区间左端点 l 越来越小，一定不可能在 [1, l] 中出现 $k_{j}=i$ 的存在。

7-15

Process

T1开场切了，T2搞了好久，T3没时间搞了

100 + 100 + 25 = 225

T1

显然答案一定是某个位置与其目标位置之间的区间

随便统计下答案就行了

T2

[最短路]

在某个点$(x, y)$，只有两种决策方式

1. 往四个方向走一步
2. 往四个方向中的两个方向扔传送门，然后往其中一个传送门走，从另一个传送门出来

跑最短路即可

T3

[三分] [树状数组]

考虑枚举最大值位置，然后确定其高度。显然代价随高度是一个单峰函数，可以三分。于是要快速计算三分出的最大值$val$在位置$i$时的代价

注：以下的$i$表示枚举出的最大值位置

题目的限制$h_j= h_i - |i - j|$可以转化成

$\begin{cases} h_j - j = h_i - i~~~(j < i)\\ h_j + j = h_i + i~~~(j > i) \end{cases}$

设初始的高度为$v_j$，最终方案的高度为$h_j$，那么我们就是要求$\sum{|v_j - h_j|}$

同样的，它可以化成

$\begin{aligned} &\begin{cases} |(v_j - j) - (h_j - j)|~~~(j < i)\\ |(v_j + j) - (h_j + j)|~~~(j > i) \end{cases} \\\\ \Rightarrow &\begin{cases} |(v_j - j) - (h_i - i)|~~~(j < i)\\ |(v_j + j) - (h_i + i)|~~~(j > i) \end{cases} \\\\ \Rightarrow &\begin{cases} \begin{cases} (v_j - j) - (h_i - i)~~~\Big((v_j - j) > (h_i - i)\Big)\\ (h_i - i) - (v_j - j)~~~\Big((v_j - j) < (h_i - i)\Big) \end{cases}~~~(j < i)\\ \begin{cases} (v_j + j) - (h_i + i)~~~\Big((v_j + j) > (h_i + i)\Big)\\ (h_i + i) - (v_j + j)~~~\Big((v_j + j) < (h_i + i)\Big) \end{cases}~~~(j > i) \end{cases} \end{aligned}$

两个树状数组，一个维护前缀信息，以$v_j - j$为下标；一个维护后缀信息，以$v_j + j$为下标

7-16

NOI Day1 网络同步赛

T1写了70分暴力挂成65，T2 T3都是裸暴力

7-18

NOI Day2 网络同步赛

搞了一上午T1的K-D Tree，T3写了暴力，T2暴力dp没写完

晚上把T2 40分暴力写了

7-19

Process

开场写了T2，然后想了很久的T1。T3暴力一个小细节写挂。。。

95 + 100 + 0 = 195

T1

[容斥] [二分图] [动态规划]

题目要求没有不合法位置的排列个数，考虑容斥，转化求至少有$i$个位置不合法的方案数

$ans = \sum_{i=0}^{n}(-1)^i(n - i)!\times f[i]$

其中$f[i]$表示钦定$i$个位置不合法的方案数

通过观察发现，不合法的情况中，每个位置和权值的对应关系如下图：

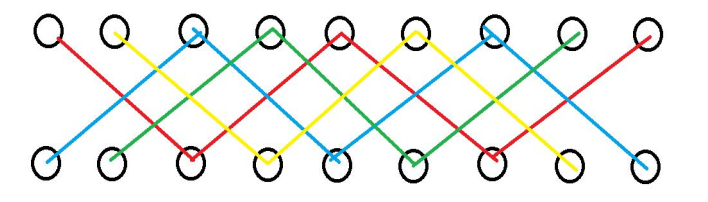
显然，钦定$i$个位置不合法就是从图中选出$i$条边，且这个边集必须是一个匹配

由于这个二分图是由若干条链构成的，于是可以把链一一提出来，排成一排做dp

因为最多只可能相邻的两个点之间有连边

$dp[i][j][0/1]$表示到第$i$个点，选出了$j$条边，当前这个点和它前面的点之间是否有连边的方案数

T2

[树状数组]

我的做法和标程稍微有点不一样

类似于共价大爷游长沙的做法，给每条非树边连接的两个点一个权值，树状数组维护，求子树权值异或和即可

T3

本以为是一道披着多项式外衣的斗地主题,最后才知道其实是一道披着斗地主外衣的多项式题

---

晚上把自己T2的std和题面写了。myy的题是真的仙

打算多搞一点T2的部分分

7-20

Process

早上去搞了牙齿，到机房已经9:00了。先花了40分钟左右写完了T1（还是有点慢），然后写了T3的$O(n\log^2n)$的做法，卡了下常就没时间了。T2只写了个暴力

T1

考虑在旋转的时候答案会如何变化

显然，有些位置上的答案会$+1$，有些会$-1$，但是我们并不需要知道这些位置到底是什么

直接用两个变量动态维护需要$+1$的位置的数量，和需要$-1$的位置的数量即可

因为每个数最多只会改变一次贡献的正/负，随便存起来搞下就行了

T2

[线段树] [数据结构]

线段树维护矩阵

线段树的$[l, r]$上维护$f[i][j]$表示从$(i, l)$走到$(j, r)$的最少步数，随便合并

T3

$O(n\log^2n)$的暴力

枚举答案区间中的最小值，分别往左右二分扩展即可

---

想今天把自己的题搞完，不知道搞不搞得完

显然搞不完啊。。。

7-21 ~ 7-28

去海南浪

期间把自己的题数据造完了

课件开了个头，基础知识点基本写完了

7-29

调beamer样式调了好久

课件搞了一点点

7-30

上午把课件写了$\frac{3}{4}$

下午又调了好久beamer样式

晚上大体把课件搞完了

7-31

上午看了哪吒

下午调整了下课件的一些小细节，正式收工