2019年6月

[Summary]

搞颓记录

6-2

难得一次能AK，以后这种比较简单的考试也要多想正解/高分部分分

100 + 100 + 100 = 300

T1

[数论] [gcd] [欧拉函数]

先考虑枚举gcd，把限制缩紧，有$(a', b')=1$，然后再化式子

一个比较有用的结论：

满足$\begin{cases}a+b=n\\ (a, b)=1\end{cases}$的$a, b$的对数就是$\varphi(n)$

$\begin{aligned} &(a, b) = 1\\ \Rightarrow &(a, a+b)=1\\ \Rightarrow &(a, n)=1 \end{aligned}$

T2

[树状数组] [计数]

最长上升子序列计数

用线段树/树状数组求LIS的时候顺便记一下方案数即可

T3

[动态规划] [前缀和]

分情况讨论，前缀和优化dp

Solution

很容易得到一个$O(n^3)$的做法（枚举lca深度， 分别枚举左右两侧链长）。写出这个暴力后可以发现，在枚举两侧链长之后，lca深度范围就确定了，于是可以用前缀和直接算

6-6

花了很长时间在想T1正解，结果部分分都没写完。T2比较简单，之前做过。T3想了一会儿，离正解已经很近了，但是最后一步没有想清楚：中间某一部分的机器人是一定能被选出来的

40 + 100 + 60 = 200

T1

[概率和期望]

考虑题目式子的具体意义，然后转化成一个概率模型（虽然正向推几乎不可能想到。。。

要大胆猜结论。。。

T2

[构造]

比较巧妙的构造，主要难在四联通条件的处理

Solution

T3

[动态规划]

通过一些特殊的状态进行dp

Solution

因为所有机器人是一起移动，相对位置不变，那么可以看成只移动出口，并且存活的机器人的范围跟着出口在一起变化
任意时刻存活的机器人的范围一定是一个矩形，于是可以以这个矩形作为状态进行dp
要发现一个性质：当前状态下有一部分区域是一定能获救的（即救这个区域内的机器人不会改变存活的机器人的范围）
需要注意的是，已经获救的机器人$\ne$当前状态下一定能获救的机器人$\ne$当前状态下存活的机器人

6-16

题目比较迷，尤其是T3。T2挂了分

100 + 80 + 100 = 280

T1

[prufer序列] [计数]

方案对应无根树形态，根据prufer序，答案为$n^{n-2}*(n-1)!$

T2

[数论] [欧拉函数] [Pollard Rho]

答案为$\varphi(n)$，根据这里的知识直接计算即可， 需要Pollard Rho大数质因数分解

T3

没有奇环没有偶环的连通图就是树。。。

6-17

题面垃圾，题解垃圾，自己太菜了

60 + 50 + 30 = 140

T1

数学题，没看懂

T2

[树状数组] [动态规划]

傻逼题不会做

Solution

很容易想到一个做法：从左往右移动长度为$L$的区间，预处理右边部分的dp数组，左边的动态处理，动态更新答案
需要注意到一个性质：假设当前删除区间为$[x, x + L]$，那么只需要看$a_{x+L+1}$是否对答案产生贡献，因为再后面的数显然此时不会更优

T3

狗屎分块，std有300L

6-20

Process

T1

点分治？

对于每种不同的深度，它们对答案贡献的增量不同，如何解决这个问题？

必须要支持把深度数组平移的操作

T2

$dp[i][j]$表示长度为$i$的排列中，有$j$个逆序对的方案。枚举下一个数填什么转移，$O(n^3)$

优化一下可以到$O(nk)$，常数是$2$，好像能跑过。。。

容斥？

不会。。。

T1无限接近正解，还是差了点

然后T1暴力也挂了。。。

39 + 57 + 33 = 129

T1

[点分治] [FFT]

不必考虑增量，显然把深度数组平移这个操作可以用FFT来实现。。。

考试的时候还忽略了一个问题，这个点分治并不能像平时一样，必须先算分治中心整棵子树的答案，再分别对应减去各个儿子对应子树的答案

T2

[容斥] [动态规划] [组合数学]

把$k$拆分成在每一位对答案的贡献，然后容斥dp

因为第$i$位对逆序对总数的贡献范围在$[0, i)$间，于是可以转化为，选出$n$个数$a_i$，满足

$\begin{cases} \sum{a_i} = k\\ \forall i, 0\le a_i < i \end{cases}$

先不考虑下面的限制，如果只有上面的限制的话显然答案就是插板法$\binom{n + k -1}{n-1}$

下面的限制可以通过容斥来满足，暴力容斥的话是枚举至少有多少个数不满足条件

$\displaystyle \sum_{i=0}^{k}(-1)^{i}\sum_{S, |S| = i}\binom{n-1+k-\sum{S}}{n-1}$

显然只关心$|S|$和$\sum{S}$

即$\displaystyle \sum_{S}(-1)^{|S|}*\binom{n -1 + k - \sum{S}}{n - 1}$

再变换一下，考虑对于相同的$\sum{S}$，统计出$\sum{(-1)^{|S|}}$

设$f_{i,, j}$表示$|S| = i, \sum{S} = j$的方案（方案即为$\sum{(-1)^{S}}$的系数，这里考不考虑符号都无所谓，如果考虑的话最后统计答案的时候就不需要考虑了）

这个dp很巧妙，首先因为每个数互不相等，那么可以强制状态中每个数是按照从大到小严格单调的来保证。

$f_{i, j} = f_{i, j - i} + f_{i - 1, j - i} - f_{i - 1, j - n - 1}$

考虑要么把当前所有的数全部+1，要么在这个基础上在后面新加一个1

但是这样第一个数可能会等于$n+1$，所以要把第一个数为$n+1$的情况减掉

发现$|S|$是$O(\sqrt k)$级别的，所以dp是$O(k\sqrt k)$的

总复杂度$O(n + k\sqrt k)$

6-22

Process

T1

作差分？

倍增？

显然，只有某一段的差分均为$d$的倍数，才有可能有值

离线？

$\frac{\max - \min}{d} - r + l$

假设从$l$到$r$的所有差分均为$d$的倍数，那么这一段的答案为

$\frac{\sum{\max} - \sum{\min}}{d} - \sum{r} + \sum{l}$

差分不为$d$的部分把原序列划分成了若干个连续段，预处理出这些连续段的答案，然后在每次端点处单独讨论一下即可

能快速求出$\sum\max,\sum\min$吗？

单调栈？离线？

HNOI2016 序列。。。

一整场考试在T1，开场30mins左右想到了一个似乎是正解的做法，写到考试结束前1个多小时才发现是假的，区间内数不能重复这个条件没想到，于是光荣爆炸，后面两题看都没看

35 + 16 + 0 = 51

T1

[扫描线] [单调栈] [线段树] [数据结构]

只有满足以下条件的区间$[l, r]$才合法：

• 没有重复元素
• 所有元素模$d$同余

其贡献为

$\frac{\max - \min}{d} - (r - l)$

于是需要维护所有可行区间的，并且求和

转化成一个经典套路：扫描线 + 单调栈 + 线段树维护历史版本和

具体来说，按右端点排序，对于所有左端点，用一棵线段树维护以当前扫到的位置为右端点的答案

对于，需要用单调栈维护，在线段树上区间加减

同时，因为右端点在移动的过程中，会有一段连续的左端点变成不合法，于是需要支持线段树上置0操作

最后，因为对于每个左端点，要维护扫过的所有右端点的答案和，所以需要线段树维护历史版本和

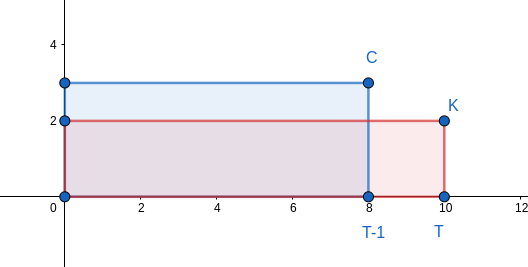
形象理解一下：

一开始答案是蓝色矩形的面积，即$C * (T-1)$

假设在$T$时刻该点权值变为$K$，那么答案就是蓝色和红色矩形的面积并，也就是$T*K + (C-K)*(T-1)$

因为权值变化量$\Delta = K-C$，那么化简一下，对于之后的某个时间$i$，其答案即为$i*K - \Delta(T-1)$

维护$K$和$\sum{\Delta(T-1)}$即可

T2

神题。。。不想写sol了。。。

看谁写了直接蒯过来吧

UPD gc写了sol，已经放在文件目录下了

T3

题解写得很清楚，观察性质一个个部分分往上做就行

6-23

Process

T1一开始想打表，发现最多才只能卡到68K左右，懒得搞了，观察了一下，发现当$n > \log(m)$时答案就是$\log(m)$（仔细想想发现也是），剩下的跑暴力就能过了

T3写了好久暴力，最后情况还是没考虑全，爆零

100 + 40 + 0 = 140

T1

[动态规划]

随便搞

T2

[交互]

这里链的情况保证了根为链的端点。。。直接stable_sort

二叉树的情况：

先随便找个点，遍历每个点，如果有祖先就跳到过去，这样就能$O(n)$求出根了。同理，用这个方法就能求出根的两个儿子，递归处理即可

T3

[计算几何] [扫描线]

树剖 + 扫描线 + 计算几何

尝试了用解析几何的方法写计算几何，感觉还行，这道题也就调了一上午

6-24

Process

T1想了好久，T3考过原题，T2没时间看了

100 + 44 + 100 = 244

T1

[贪心] [长链剖分]

类似于长剖的过程，贪心地把树划分成若干条链，取前$k$大的链即可

T2

权值$\le 75$

线段树暴力维护信息

T3

[最短路] [状态压缩] [动态规划]

差分，转化成求$2k$个起点，$nm$条边的最短路，最后状压dp