「Algorithm」对子集和DP/高维前缀和的一些理解

太菜了，想半天才想清楚

Description

每个集合有个权值，对于每个集合求它所有子集的权值和

Solution

暴力枚举子集是$O(3^n)$的，但是我们可以通过高维前缀和做到$O(2^nn)$

先放代码

for (int i = 1; i <= N; ++i)
    for (int state = 0; state <= ALL; ++state)
        if (state & (1 << (i - 1)))
            Add(Ans[state], Ans[state ^ (1 << (i - 1))]);

为什么要外层循环枚举新加的元素，内层枚举状态呢？

为什么这样能做到不重复计算呢？

考虑下图这样的转移

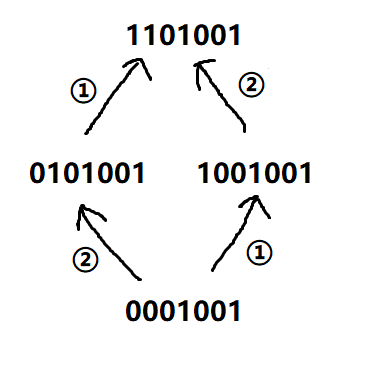
显然，因为先枚举的转移哪一位，所以标①的两个一起转移，标②的两个一起转移

假设①比②先转移，那么$0001001$只会从$0101001$转移到$1101001$，而不会从$1001001$转移过去（因为从$1001001$转移的时候，$0001001$还没转移到$1001001$上）

这样相当于给转移的每一位钦定了顺序，必须把某一位全部转移完再考虑下一位。而且外层按任意顺序枚举都可以

同理，因为对于某一位而言，只可能是从$0$转移到$1$，所以内层的状态也可以按任意顺序枚举

只要保证外面枚举哪一位，里面枚举状态就行