这个东西比较简单，复杂度又不会证（好像是假的），那就随便写一点吧

Brief Introduction

k-d tree是用来解决高维空间内一些操作的数据结构，OI中一般只用二维，下面都默认指二维

它大概长这样子：

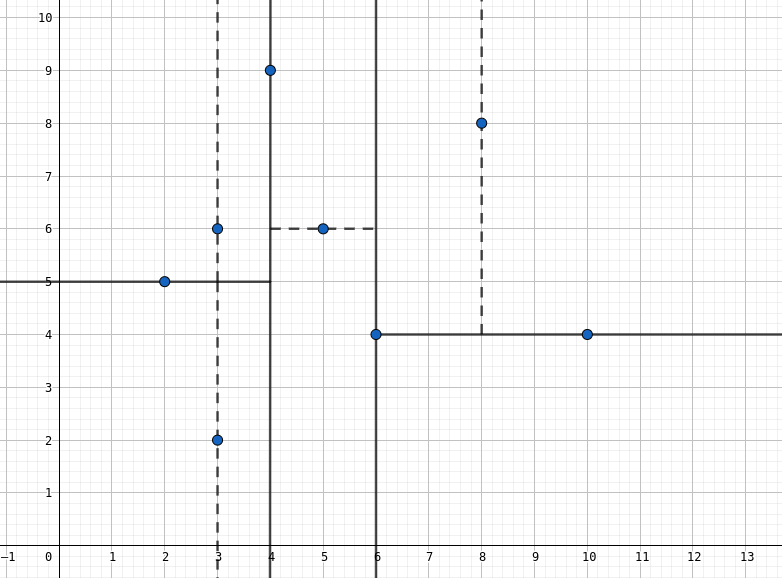
19-3-24-1

简单来说，它是一棵二叉树的结构，每个节点代表了平面上的某一个部分

每次分叉的时候按照水平或竖直把当前部分分割成两半，直到平面内只剩一个点

构建

  • 确定当前平面内所有点极差最大的那一维
  • 按照这一维把所有点排序，找到中点，这一步可以用nth_element函数实现
  • 从中点把平面分割成两部分，递归处理

如果需要动态插入的话，还需要像替罪羊树一样动态拍扁重建

应用

最邻近查询

这一部分好像复杂度有问题，相当于是暴力加上了一些减枝

  • 模拟插入的过程，找到待查点在树上哪个节点所包含的部分，用经过的点与待查点的距离更新答案
  • 回溯的时候，如果当前点的另一个儿子有可能使答案更优，则访问另一个儿子

二维区间操作

我感觉这个复杂度应该是对的。。。

相当于把线段树扩展到二维，支持二维区间的一些操作。某些时候可以代替树套树/二维线段树，空间是O(n)O(n)的，更加优秀

这个很好理解，与线段树几乎一模一样

代码见此

19-9-29 UPD

KDT的复杂度显然是错的。。。

因为在递归的时候走到的节点不一定有用，即有可能一开始走到某个节点的时候，发现它可能可行，但递归到很深的地方的时候才发现不可行。这样就会浪费很多时间。所以并不是log\log的

正因为这个原因，KDT在实现的时候不能这么写：

1
2
3
4
5
6
inline void update (int o, int l, int r, pii x, pii y)
{
    ++node[o].sum;
	if (blabla) return ;
    update (lson), update (rson);
}

而应该这么写：

1
2
3
4
5
6
7
inline void update (int o, int l, int r, pii x, pii y)
{
    if (blabla) return ;
    if (balbla) return void (++node[o].sum);
    update (lson), update (rson);
    push_up (o);
}