「Codeforces」一些题

最近做的一些别人都一眼秒掉的题

近几场CF里一些别人都一眼秒掉的题

里面没有代码，代码可以见CF提交记录

CF1137A Skyscrapers

Description

给定一个$n*m$的网格，每个格子里都有一个数，对于任意一行和任意一列

要求把这$n+m-1$个数重新用正整数编号，并且对于这一行，数与数之间的大小关系不变，对于这一列同理

求出任意一行和任意一列编号使用的最大编号的最小值。

$n, m\le 1000$

Solution

每一行每一列分别离散，并记录离散之后的值，每次看是选行的值作为最终的值还是列的值作为最终的值，分别算一下即可

CF1137B Camp Schedule

Description

给出两个01串$S$和$T$

把$S$打乱顺序，使得$T$在$S$中出现的次数最多

$|S|, |T|\le 500000$

Solution

$S$没有什么用，只要记录下01的个数。对于$T$跑一下KMP，每次跳fail贪心放就行了

CF1137D Cooperative Game

Description

交互题

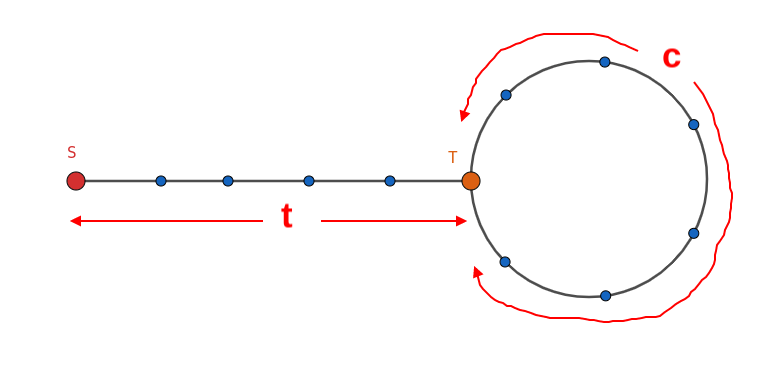
有一张图是由一个长度为$t$的链和一个大小为$c$的环中间连上一条边组成的

假设环与链交界的位置为$T$，链的左端点为$S$

现在在$S$处有$10$个棋子，编号$0-9$，每次你可以让任意数量的棋子向出边方向走一步，交互库会返回若干个集合，每一个集合内的棋子都在同一个位置上，并且这个位置上的所有棋子都在这个集合中

现在你既不知道$t$也不知道$c$。你需要使用不超过$3(t+c)$次操作使得所有棋子都移动到$T$位置上并且返回交互库done。

Solution

好妙的一道题

首先考虑类似floyd判圈的做法，移动两个棋子，分别以1步/轮和1步/2轮的速度往前走，一直走到两个棋子相遇为止

注意到，当第二个棋子走了$2t$轮到达$T$点时，那么第一个棋子肯定会走到环上从T开始逆时针标号的$t$位置

所以第一个棋子还需要走$c-t$步才能追上第二个棋子，追上的位置为$c-t$

那么追上之后，这两个点距离$T$点还有$t$步，剩下的点距离$T$点也还有$t$步，把所有棋子都移动$t$步即可

CF1137E Train Car Selection

Descrption

你有一列有$n$个车厢的火车，从车头开始$1-n$编号，一开始所有车厢的价值都是$0$(包括中途加入的车厢)

有$m$次操作，分为$3$种：

• 在车头位置加入$k$节车厢
• 在车尾位置加入$k$节车厢
• 修改每节车厢的价值：每次修改会给定$s,b$，如果当前车厢是从车头开始数的第$i$节，那么它的价值就会加上$(i-1)*s+b$

在每次操作结束之后回答价值最小的车厢的编号以及其价值。如果有多个输出编号最小的那个

$n\le10^9, m\le 300000$

Solution

首先发现每次加进来的一段车厢只有最左边的那个可能成为答案；且如果在前端插入一段，那么后面全部都没用了，可以直接丢掉

接下来考虑每次往后面加一个点的情况

显然，如果$a$在$b$的左下方（$x_a < x_b, y_a < y_b$），那么无论什么时候$a$一定比优

那么可能成为最优解的点的坐标一定是单调下降的

考虑横坐标位于$A$和$C$之间的$B$，它如果要成为最优解要满足什么条件

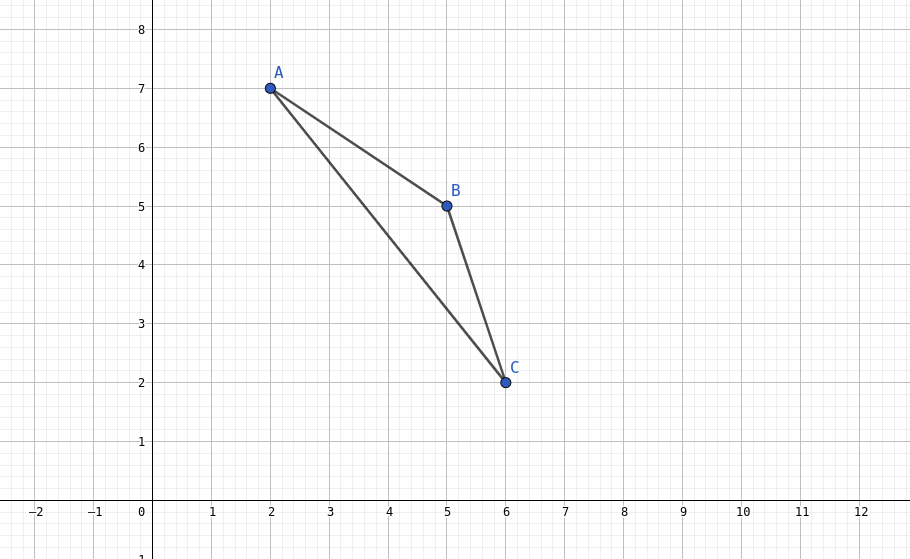
假设当前加上的是一条$y=kx+b$的直线

那么$\Delta y_B - \Delta y_A = k(x_B - x_A)$，也就说明$B$比$A$多增加了$k(x_B - x_A)$。它必须小于$y_A - y_B$，$B$点才会更优

于是$\displaystyle k(x_B - x_A) < y_A - y_B \Rightarrow k < -k_{AB}$

类似地，若$B$比$C$优的话就要满足$k > -k_{BC}$

注意到，若$B$不在左下凸壳上的话（图中所示情况），则$k_{AB}> k_{BC}$，此时$k$无解

因此，只有左下凸壳上的点才有可能成为最优解，单调栈维护一下即可

CF1120A Diana and Liana

Description

给定一个长度为$m$的序列，你可以从中删去不超过$m-n*k$个元素，剩下的元素从左往右每$k$个一组，最后一组可以不满

给定你一个大小为$|S|$的可重集，要求你分出的组中至少有一组构成的可重集包含了给定的可重集。

构造一种符合条件的删数方案。

$n,m,k,|S|\le5*10^5$

Solution

考虑对于每一个右端点求出一个最大的左端点恰好包含集合$S$，显然可以用two pointers做到$O(n)$，然后判断这个区间$[l, r]$是否合法

这里调了我一年，最后看了yyb博客，强制$r-l+1\ge k$之后就过了。。。

CF1120C Compress String

Description

给出一个串$S$，你需要把它进行划分

有两种划分方式：要么是一个字符成一组，代价是$a$；要么是$[l,r]$划分一组，要求$[l,r]$是的一个子串，代价是$b$。

求最小代价。

$|S|\le 5000$

Solution

建SAM直接刷表dp即可

CF1136E Nastya Hasn't Written a Legend

Description

给你一个长度为$n$的序列$a_1\sim a_n$和一个长度为$n-1$的序列$k_{1}\sim k_{n-1}$

有$q$次操作，分为两种

• 给第$x$个数$+y$ 然后对于$i \ge x$执行一段连续操作：$a_{i+1} = max\{a_{i+1}, a_i + k_i\}$
• 查询区间和

Solution

显然每次有效的Chkmax操作只会是从$x$开始的一段连续区间，区间的右端点可以二分得到，接下来考虑如何维护这个东西

发现题目的限制可以转化为这样：

于是对于每个$i$，直接用线段树维护这个$a_i - \sum_{j=1}^{i-1}k_j$即可，每次修改都是区间set(赋值)操作