「Algorithm」欧拉回路

欧拉回路学习笔记

一些定义

欧拉路径

图中的某一条路径经过每条边恰好一次，则该路径称为欧拉路径

注：哈密顿路径：图中的某一条路径经过每个点恰好一次

欧拉回路

一条闭合的欧拉路径

不难发现，欧拉回路一定是形如若干个环套在一起

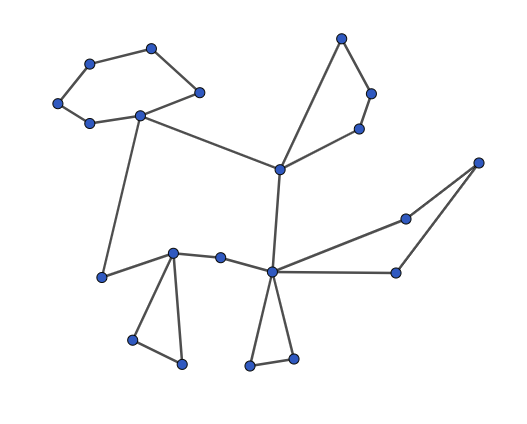
当然，还可以再多两个“线头“出来

判定

欧拉路径

1. 图连通
2. • 无向图：奇点数为0或2，并且这两个奇点其中一个为起点另外一个为终点
   • 有向图：可以存在两个点，其入度不等于出度，其中一个入度比出度大1，为路径的起点；另外一个出度比入度大1，为路径的终点

欧拉回路

1. 图连通
2. • 无向图：奇点数为0
   • 有向图：每个点的入度等于出度

求出一条欧拉回路

上面的图已经很形象地展示了，欧拉回路是形如若干个环套一起的

那么考虑用一个栈在dfs过程中来存这个欧拉回路，具体流程如下（直接上代码了）：

inline void dfs (int x)
{
	for (int &i = Begin[x]; i; i = Next[i])
	{
		int y = To[i];
		if (Vis[i >> 1]) continue;
		Vis[i >> 1] = 1;
		dfs (y);
	}
	idfn[++dfs_clock] = x;
}

每走过一条边的时候把这条边标记一下，一直走到不能走为止（即走到了某个环的终点），最后取dfs后序遍历

注意要加当前弧优化，否则可能会被卡