一个连tarjan都想不清楚的菜鸡

Tarjan

low[x]表示xx子树中的点通过非树边能到达的，仍在栈中的，dfs序最靠前的点的编号

是用来求强连通分量/点双/边双最重要的一个东西

下面的东西都放到dfs树上就很好理解了

强连通分量

有向图

强连通图：任意两点互相可达

强连通分量：图中的一个极大强连通子图

显然，任何一个强连通分量，必定是对原图的dfs树的子树。那么我们只要确定每个强连通分量的子树的根，然后根据这些根从树的最低层开始，一个一个拿出强连通分量即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
inline void tarjan (int x)
{
	Stack[++top] = x, In[x] = 1;
	dfn[x] = low[x] = ++dfs_clock;
    
	for (int i = Begin[x]; i; i = Next[i])
	{
		int y = To[i];
		if (!dfn[y]) tarjan (y), Chkmin (low[x], low[y]);
		else if (In[y]) Chkmin (low[x], dfn[y]);
	}
	
	if (dfn[x] == low[x])
	{
		++scc_cnt;
		while (1)
		{
			int a = Stack[top--];
			Belong[a] = scc_cnt, In[a] = 0;				
			if (a == x) break;
		}
	}
}

点双

无向图

割点：去掉这个点后原图改变了原图的连通性

点双连通图：没有割点的图

点双连通分量：极大的点双连通子图

  • 每存在一个割点就会把图分成若干个点双，每个割点至少属于两个点双
  • 点双内的任意两点至少有两条不经过重复点（除起点和终点）的路径

显然，如果一个点的子树中能返回到的最早的节点的dfs序大于等于当前点的dfs序，则子树中的点走到外面去一定会经过这个点，所以去掉这个点后原图就不连通了，于是它是一个割点

注意需要记录dfs树中的父亲节点，显然low值不能通过父亲节点去更新

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
inline void tarjan (int x, int f)
{
	dfn[x] = low[x] = ++dfs_clock, Stack[++top] = x;

	for (int i = Begin[x]; i; i = Next[i])
	{
		int y = To[i];
		if (y == f) continue;
		if (!dfn[y]) tarjan(y, x), Chkmin (low[x], low[y]);
		else Chkmin (low[x], dfn[y]);
	}

	if (low[x] >= dfn[f])
	{
		while (1)
		{
			int a = Stack[top--];
			In[a] = 0;
			if (a == x) break;
		}
	}
}

如果需要求割点的话还要特判一下根结点的情况

左图根不是割点，右图根是割点

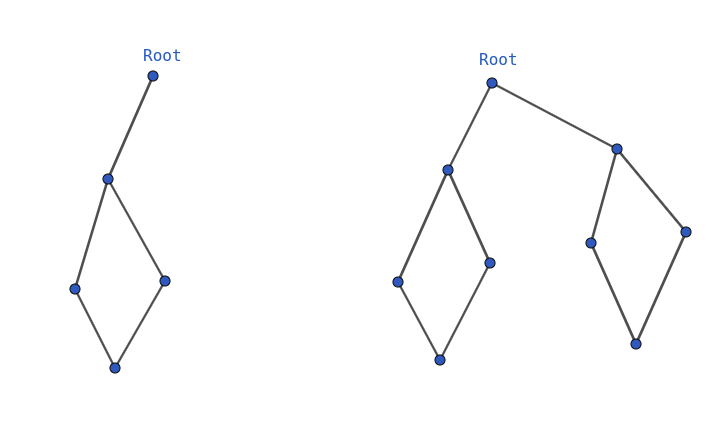
19-3-13-1

处理方法：求出一个割点xx时令cnt[f]++，最后看cnt[root]是否大于11即可

边双

与点双定义类似

无向图

割边（桥）：去掉这条边后原图改变了原图的连通性

边双连通图：没有桥的图

边双连通分量：极大的边双连通子图

  • 每存在一个桥就会把图分成若干个边双，桥不属于任何一个边双
  • 边双可以看作原图把所有桥都去掉分成的若干个连通块
  • 边双内的任意两点至少有两条不经过重复边的路径

显然，边双的范围比点双要小，限制更严。只有一个点子树中能返回到的最早的节点的dfs序大于当前点的dfs序，这个点与它父亲的那条边才是桥

注意需要记录父亲到它的那条边的编号，因为如果存在重边的话就能通过重边走到父亲节点，这是合法的。只需要保证接下来走的边不是来的那条边即可

代码和点双类似，把low[x] >= dfn[f]改成low[x] > dfn[f]即可

写法上的细节

点双判断low[x] >= dfn[f]那里写里面外面都可以；边双只能写外面。所以干脆都写外面就好了

因为边双如果不写外面就不能判断根节点所在的边双了，根结点那里实际上还是有一条父亲边

应用

点双和边双在应用时，往往是利用到了任意两个点之间有两条（不经过重复点/边的）路径这个性质

  • 求仙人掌中的环是缩点双（任何一条边不属于两个环中，那么一定都是简单环，但一个点可能属于两个环中）

  • 求仙人球（任意一个点不属于两个环中）的环是缩边双

  • 圆方树

好像差不多了吧