斜率优化学习笔记

关于斜率优化这个玄学东西一些自己的bb理解（似乎和网上的理解方法都不太一样？）

分割线以下写的东西都是假的 不要看！！！

UPD 19-8-11 最一般的斜率优化

$dp[i] = \min_{j < i}\{a[i] * b[j] + c[i] + d[j]\}$

保证$a[],b[]$都单调递增（不管$a[]$本身是不是单增，都可以通过移项变成单增形式）

考虑两个决策$j,k$,且$j < k$，若$j$比$k$优，那么式子最终会化成

$\frac{d[j] - d[k]}{b[j] - b[k]} ~?~a[i]$

其中$?$处可能是$>$，也可能是$<$

斜率优化的本质是利用决策单调性，即在某时刻决策$j$比$k$优，那么在之后的任何时刻都要满足$j$比$k$优

又因为$a[i]$单增，因此这里必须是$<$。如果为$>$的话，要把限制条件j比k优改成k比j优

对于这两种不同的限制条件，需要用不同的数据结构维护：

• $j < k$，且$j$比$k$优：单调栈（弹后面）
• $j < k$，且$k$比$j$优：单调队列（弹队首）

因为要把更劣的决策弹掉

再考虑要维护上凸壳还是下凸壳：

• 单调栈：弹后面，因此要满足斜率单降，上凸壳
• 单调队列：弹队首，因此要满足斜率单增，下凸壳

以单调栈为例：

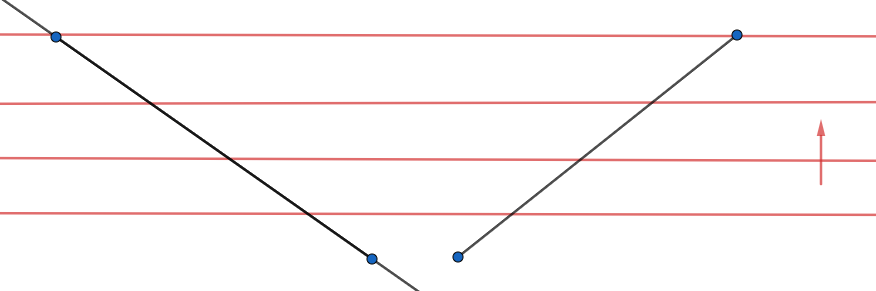
红色的线代表上面的$a[i]$，它自下而上单增

左边是斜率单减，右边单增

如果是右边的情况，斜率单增的话，那么只有在最上面那根线的时候才会一次性把栈里的东西弹掉，显然不行

（注意这里是如果当前直线满足的话，就把该直线下面的所有点都弹掉）

总结一下流程：

设$j < k$化式子，保证$a[i]$单增

• $j$比$k$优$\rightarrow$单调栈$\rightarrow$上凸壳
• $k$比$j$优$\rightarrow$单调队列$\rightarrow$下凸壳

---

基本形式

$dp[i] = \min_{j < i}\{a[i] * b[j] + c[i] + d[j]\}$

其中$b$具有单调性（假设$b$单增）

假设我们有两个决策$j,k(k < j)$，且对于$i$而言，在$j$的决策比$k$优，那么有

$\begin{aligned} &a[i] * b[j] + c[i] + d[j] < a[i]*b[k] + c[i] + d[k]\\\\ \Rightarrow &a[i](b[j] - b[k]) < d[k] - d[j]\\\\ \Rightarrow &\frac{d[k] - d[j]}{b[j] - b[k]} > a[i]\\\\ \Rightarrow &\frac{d[j] - d[k]}{b[j] - b[k]} < -a[i] \end{aligned}$

不难发现，如果$j,k$满足这个条件的话，那么$j$的决策比$k$优

记$Slope(j, k) = \frac{d[j] - d[k]}{b[j] - b[k]}$，把$b$看作横坐标，$d$看作纵坐标。

因为当前的$-a[i]$是固定的，所以对于某一个决策$k$而言，如果某个在它后面的决策$j$比它优，在图像上来看就是$j$点在斜率为-a[i]，且过k点的直线(也就是下图中的红色直线)的下方

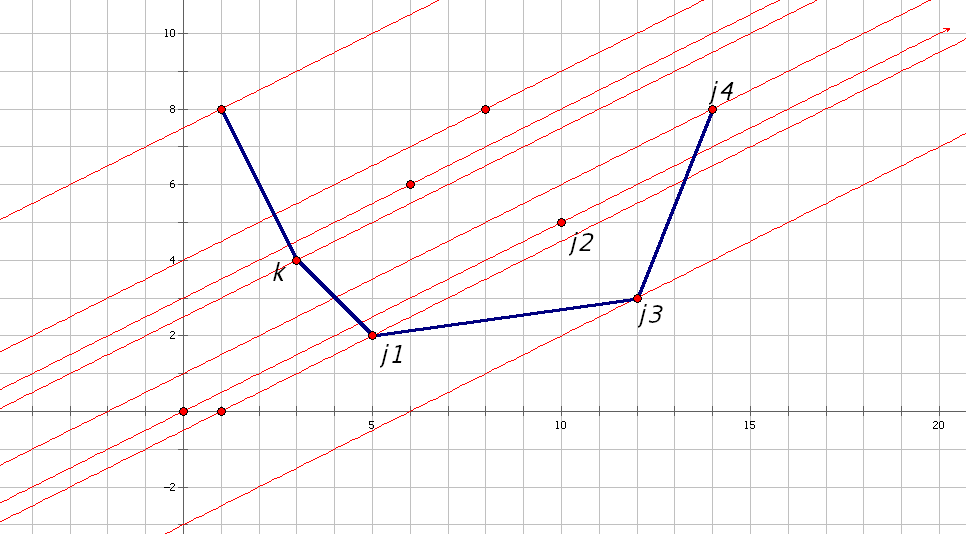
继续观察发现，对于像$j_2$这种不在下凸壳上的点，无论$-a[i]$为多少，它一定不会是最优决策

证明：

1. 若$j_2$决策比$k$劣那显然$j_2$不是最优
2. 若$j_2$决策比$k$优（即上图所示情况），则$j_3$的决策一定比$j_2$优，因此$j_2$肯定不为最优

因此，最优解一定出现在下凸壳上，我们可以用单调栈维护凸壳

但是，下凸壳上的哪个点才是最优的呢？

不难发现，最优解$x$一定满足$Slope(x - 1, x) < -a[i]$且$Slope(x + 1, x) > -a[i]$

也就是说，$-a[i]$刚好夹在它与前后两个点的斜率之间

通过图像感性理解，其实就是把一条斜率为$-a[i]$的直线从无穷小处移过来，于凸壳第一个相交的点

因为这个点往左/右走的话，斜率一定会分别变小/变大，而这两种情况都会使得答案更劣，于是这个交点就是最优解

特别地，如果$-a[i]$单调递增，可以直接用单调队列维护，直接把队首小于$-a[i]$的不断弹出即可

否则就必须在单调栈上二分查找

乱bb一些东西

自己理解来看，斜率优化在优化dp转移时，主要是两个部分。首先根据斜率的一些性质建立出凸壳，去掉了很多不需要的转移，并且使得有用的转移是斜率单调的。然后对于每次转移，就只需要在凸壳上二分斜率，或是直接维护单调队列，用指针扫一下即可。

这段东西都是自己瞎bb的，要是理解错了就gg了。。。

更一般的情况

上面的式子中，如果$b[i]$也不单调的话，就需要用Splay维护动态凸包/CDQ分治优化解决了

一般来说直接写分治会更加简便灵活，这个东西也类似于一个三维偏序，一维下标要满足$j<i$；一维$b[]$要满足在静态的时候单增；还有一维是斜率$-a[i]$

与分治有关的部分在这里也提到过，这里就重点写下计算贡献的过程

考虑用$[l,mid]$中求出的dp值去更新$[mid+1,r]$的dp值：

由于这个子问题已经是静态的了，顺序对此时的贡献是没有影响的，于是可以直接排序

对于$[l,mid]$中的所有决策点按$b[]$排序，可以线性构造出这个凸壳

再对$[mid+1,r]$中的状态按斜率排序，这样又能线性在凸壳中找到最优点

总复杂度$O(n\log^2 n)$，写归并排序的话是$O(n\log n)$的