题目链接：传送门

Description

We have a pyramid with N steps, built with blocks. The steps are numbered 1 through N from top to bottom. For each 1≤i≤N, step i consists of 2i−1 blocks aligned horizontally. The pyramid is built so that the blocks at the centers of the steps are aligned vertically. Snuke wrote a permutation of (1, 2, …, 2N−1) into the blocks of step N. Then, he wrote integers into all remaining blocks, under the following rule: The integer written into a block b must be equal to the median of the three integers written into the three blocks directly under b, or to the lower left or lower right of b. 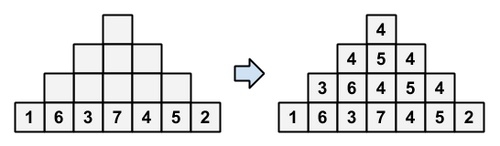Writing integers into the blocks Afterwards, he erased all integers written into the blocks. Now, he only remembers that the integer written into the block of step 1 was x. Construct a permutation of (1, 2, …, 2N−1) that could have been written into the blocks of step N, or declare that Snuke's memory is incorrect and such a permutation does not exist.

Hint

2 <= N <= 1e5 1 <= x <= 2 * N - 1

Sample Input

4 4

Sample Output

Yes 1 6 3 7 4 5 2

Solution

这题懒得翻译了，就是从下往上填格子，每个格子取它下面三个格子的中位数 显然当x==1x==1或x==2N−1x==2N - 1 时无解 然后如果x!=2x!=2 并且 x!=2N−2x!= 2N - 2的话我们可以把x放在正中间，然后把与它差的绝对值不超过2的数分列它的两侧，即x+2 x-1 x x+1 x-2这样放置。那么这样便在上一层可以产生三个相同的x，依次推上去的话一定是x 当x==2x==2或x==2N−2x==2N-2时，用类似的方法能在上一层构造出两个x，这样也能使最顶端为x

Summary

太难得能不看题解做出来一道构造题了。做这道题的时候开始思路还不是很清晰，然后尝试模拟了几组数据之后就发现了规律。以后还是要忍着不能看题解

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <bits/stdc++.h>
using namespace std;
int N, x;
int P[1000000 + 100];
int main()
{
#ifdef hk_cnyali
    freopen("B.in", "r", stdin);
    freopen("B.out", "w", stdout);
#endif
    scanf("%d%d", &N, &x);
    if (x >= 2 * N - 1 || x <= 1)
    {
        cout<<"No"<<endl;
        return 0;
    }
    int l = x - 2, r = x + 2, flag = 0; 
    if (x == 2)
    {
        l = 1, r = 5;
        flag = 1;
        if (2 * N - 1 < 5)
        {
            if (x == 2)
            {
                cout<<"Yes"<<endl;
                printf("1\n2\n3\n");
            }
            else
                cout<<"No"<<endl;
            return 0;
        }
    }
    if (x == 2 * N - 2)
    {
        l = 2 * N - 5, r = 2 * N - 1;
        flag = 2;
        if (l < 1)
        {
            if (x == 2)
            {
                cout<<"Yes"<<endl;
                printf("1\n2\n3\n");
            }
            else
                cout<<"No"<<endl;

            return 0;
        }
    }
    cout<<"Yes"<<endl;
    for (int i = 1, Cnt = 1; i <= 2 * N - 1, Cnt <= (N - 3); ++i)
        if (i >= l && i <= r) continue;
        else cout<<i<<endl, P[i] = 1, ++Cnt;
    if (flag == 1)
        printf("5\n1\n2\n3\n4\n");
    else if (flag == 2)
    {
        int m = 2 * N - 1;
        printf("%d\n%d\n%d\n%d\n%d\n", m - 3, m, m - 1, m - 2, m - 4);
    }
    else 
        cout<<x + 2<<endl<<x - 1<<endl<<x<<endl<<x + 1<<endl<<x - 2<<endl;
    //cout<<r<<endl<<l + 1<<endl<<l + 2<<endl<<r - 1<<endl<<l<<endl;
    for (int i = 1, Cnt = 1; i <= 2 * N - 1, Cnt <= (N - 3); ++i)
        if ((i >= l && i <= r) || P[i]) continue;
        else cout<<i<<endl, ++Cnt;
    return 0;
}